8

I understand that $p \Rightarrow q \Rightarrow r$ isn't defined since it might mean one of 4 different sentences:

  1. $p \Rightarrow (q \Rightarrow r)$
  2. $(p \Rightarrow q) \Rightarrow r$
  3. $(p \Rightarrow q)\land(q \Rightarrow r)$
  4. $(p \Rightarrow q)\land(p\land q \Rightarrow r)$

1), 2) While the first two make sense, because in the notation $p \Rightarrow q \Rightarrow r$ we just add brackets, but outside of mathematical logic I haven't seen them used in proofs.

3) The third option is quite common though, for example, if $x\in\mathbb{R}$ then $$|x-2|<3\quad\Rightarrow\quad -3<x-2<3 \quad\Rightarrow\quad -1<x<5$$ Another example (from page 375 of the book P. Naudin, C. Quitté, Algorithmique algébrique avec exercices corrigés, 1992): 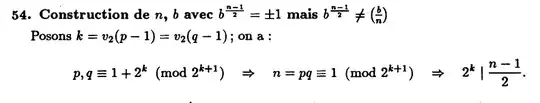enter image description here Also in this book Proofs and Mathematical Reasoning there are plenty of examples of implication chains (eg. page 13-14).

4) I don't recall if I've seen the fourth option used anywhere, but it would be so useful if we could write proofs using this notation, for example: $$x<-y^3<-1 \quad\Rightarrow\quad x<-\sqrt{y} \quad\Rightarrow\quad x^2>-x\sqrt{y}$$ A simpler example: $$1<x<2 \quad\Rightarrow\quad x<3 \quad\Rightarrow\quad 1<x<3$$ We can't write $x<3 \Rightarrow 1<x<3$ of course, but it's at the end of the chain (in text proofs this is quite common though, I mean we almost never say all the things we use for the last implication, i. e. we usually state things in sort of a chain: "if this then that, if this then that, ..., therefore we get that").

EDIT. The question is about the 4th case. Is it used by any authors? Is there a different arrow (or other symbol) notation for the 4th case?

Robai
  • 207
  • 2
    Sorry, but I see only $2$ variants $(p \Rightarrow q) \Rightarrow r$ and $p \Rightarrow (q \Rightarrow r)$. – zkutch Jun 27 '23 at 21:29
  • 1
    I don't understand your question, because you state correctly the term is ambiguous. Since $\implies$ is not associative, we could evaluate left-to-right, but there is no way, with binary operators, to get $(3).$ Why invent notation when you can already express $(3)?$ – Thomas Andrews Jun 27 '23 at 21:36
  • There is a symbol $\vdash$ (turnstile, e.g. $p\vdash q$, which means "$p$ proves $q$", "$q$ is derived from $p$". There is also $\vDash$ (double turnstile), say $p\vDash q$ means "$p$ implies $q$", "whenever $p$ is true, $q$ must be true". Both are widely used in mathematical logic but not so much in math education. –  Jun 27 '23 at 21:59
  • @Robai it depends upon what you're doing. If you're using a Type-theoretical theory or proof assistant (software) it's (1) or (2). For Lean/Coq it is (2) or right-associative. In a category where objects are propositions and arrows are implications, you have (3). Perhaps you need true props for $\circ$ (composition of arrows) to be associative though. The fourth one is kind of like a custom notation that I've never seen used, that says "build up a context" as you discover true props. – Daniel Donnelly Jun 27 '23 at 22:30
  • 1
    The context in which you see this should tell you a lot! Without such context, the fact that there are no parentheses, together with the use of $\implies$, rather than $\to$, to me suggests that I would be dealing with an implication chain, i.e. something along the lines of 3. However, I would definitely not see that as $(p \implies q) \land (q \implies r)$, because now you are mixing up a logical symbol ($\land$) with a meta-logical/mathematical symbol ($\implies$). I would just treat it as two claims $p \implies q$ and $q \implies r$ – Bram28 Jun 28 '23 at 00:14
  • Oftentimes implication is interpreted as right-associative, so $p \to q \to r$ is a shorthand for $(p \to (q \to r))$ on that interpretation. – PW_246 Jun 28 '23 at 01:56
  • @Prem I rolled back your edit because it distorts the OP's classification: firstly the Case 5 that you added is just a special case of their Case 3 (so is unnecessary), and secondly your claim that "A⇒B⇒C" is ever read as equivalent to, rather than implies, "A⇒C" is dubious (and unnecessarily strong). – ryang Jun 28 '23 at 05:47
  • 1
    @Robai I agree with your overview, disagree that Reading 4 (or a new symbol for it) is useful because in such cases using words would be much clearer, and second @Bram28's two observations (though I find only (P⇒Q)∧R, but not (P∧Q)⇒R, odd if ⇒ is agreed to be metalogical instead of the material conditional, because the former places a metalogical symbol within the object language). – ryang Jun 28 '23 at 06:00
  • Strange that you claim I DISTORTED OP Classification , @ryang , when I ensured that OP Classification remains unaltered. I added a new Case with a new Number , where I gave the "Example where it is equivalent" , not that it is "Universally Equivalent". I am not getting into roll-back-edit-war , but I disagree with your assessment. – Prem Jun 28 '23 at 06:02
  • @Prem (A classification is a structure: starter-main and starter-main-dessert are two different meal structures. Adding a dessert does not affect the first two courses but does alter the framing/understanding of the concept of 'meal'.) Yes we don't have to agree on this. – ryang Jun 28 '23 at 06:09
  • 1
    Two different contexts: (i) propositional logic, where usually the conditional connective is right-associative; thus, $p \to q \to r$ is an abbreviation for $p \to (q \to r)$. (ii) usual mathematical practice, where $\Rightarrow$ stands for "it follows that" and thus we can have a "chain" of consequences: "from A, it follows B and (from B) it follows C", where the consequence relation is transitive. – Mauro ALLEGRANZA Jun 28 '23 at 11:54
  • 2
    I have never seen the 4th case used by authors. The expression could mean any of 1,2,3,4 as long as you define it as such in your book, paper, etc. – RyRy the Fly Guy Jun 28 '23 at 15:19
  • Does this answer your question? Associativity of logical connectives – Tankut Beygu Jul 01 '23 at 08:14

1 Answers1

3

Using arrows informally in a string of implications $$ p_0\Rightarrow p_1\Rightarrow p_2\Rightarrow\ldots\Rightarrow p_n $$ I would take to mean starting with something true and going through the implications left-to-right, asserting the truth of all of these $$ p_0\land(p_0\Rightarrow p_1)\land(p_1\Rightarrow p_2)\land\ldots\land( p_{n-1}\Rightarrow p_n), $$ with the goal of asserting $p_0\Rightarrow p_n$. In other words "checking each step is correct" is being interpreted as the conjunction of the implications.

yoyo
  • 9,943
  • 2
    What do you mean by "can"? One can use symbols as one wishes as long as there is agreement about their use. My answer is how I would interpret myself when writing something like $p_0\Rightarrow p_1\Rightarrow p_2\Rightarrow\ldots\Rightarrow p_n$ on a piece of paper or chalkboard. – yoyo Jun 27 '23 at 22:18
  • 1
    @yoyo why there is $p_0$ at the start? (if $n=1$ then we have implication $p_0\Rightarrow p_1$, which doesn't need $p_0$ to be true) – Robai Jun 27 '23 at 22:47
  • For no real reason; the intention depends on context. If I want $p_n$ then I need $p_0$ in my hypothetical interpretation. – yoyo Jun 27 '23 at 23:05
  • 1
    I agree with @Robai: the string "$p_0\Rightarrow p_1\Rightarrow p_2\Rightarrow\ldots\Rightarrow p_n$", in itself, looks like it's merely an implication chain, without any assertion that $p_0$ is actually true; in other words, it appears to be indicating "$p_0\Rightarrow p_n$" rather than "$p_0,;\therefore p_n$". – ryang Jun 28 '23 at 12:25
  • I think it would be better to use good old-fashioned $\therefore$ rather than $\Rightarrow$ for this purpose. – Rob Arthan Jun 29 '23 at 20:47