A bead is moved 6 times from vertex to vertex on a steel-wire cube ; how many different ways to come back to the starting vertex?

Question

Consider an cubical arrangement of steel wire (edges made up steel wire) and a bead is on this wire (one can slide this bead across wire).A person performing a game in which there are 6 steps, in each step the bead is moved from one vertex to another adjacent vertex. In how many different games the final and initial positions of the beads are same.

I tried to make cases, that $x$ denotes displacement in $x$ axis, respectively $y$,$z$.

$$\sum^a{x}+\sum^b{y}+\sum^c{z}=0$$ where, $$a+b+c=6$$

And took $28$ cases, since it was symmetric it doesn't took more than half a hour but and gave answer 191 (my accuracy isn't good my answer might not be true).

I am completely exhausted after this counting? Can someone help me if finding a good solution for this?

Answer 1

Each move will either be in the X, Y, or Z directions. There needs to be an even number of moves in each direction, for the bead to return to where it started. Therefore, we can phrase the problem combinatorially as follows:

How many sequences of $6$ letters are there, where each letter is X, Y, or Z, such that all three letters appear an even number of times?

This question is most easily solved using exponential generating functions. In general, you can show that the number of $n$-letter words over an $m$-letter alphabet where each letter appears evenly is $$ \frac1{2^{m-1}}\sum_{k=0}^{\lfloor m/2\rfloor}\binom{m}k(m-2k)^n. $$ See this answer from Brian M. Scott for a proof using EGF's. Applying that to your problem, the answer is $$\frac1{2^2}\left[3^6+\binom 31 1^6\right]=183.$$

---

We can count the number of ways using casework as well, in a manner that takes five minutes instead of thirty. There are three cases for the number of X's in the string, each with some sub-cases.

• If there are six X's, then there is only $1$ possible word.

• If there are four X's, then there are $2\times \binom 62$ possible words. The $2$ accounts for where the other two symbols are Y or Z, and the $\binom 62$ chooses the location of these two symbols.

• If there are two X's, then we choose their locations in $\binom 62$ ways. What remains are four symbols, all of which are Y or Z, where each appears evenly.

  • There are two sub-cases where all symbols are the same, YYYY or ZZZZ.

  • There are $\binom 42$ sub-cases with two Y's and two Z's.

• If there are zero X's, then what remains is a string of an even number of Y's and an even number of Z's. This is equivalent to choosing an even-sized subset of $\{1,\dots,6\}$. It is well known that exactly half of the subsets of a finite set have even size, so there are $2^{6-1}=32$ words in this case.

  • Alternatively, you can directly count the number of ways to choose the locations of either $0,2,4,$ or $6$ Y's, to arrive at the same answer of $\binom60+\binom62+\binom64+\binom66=32$.

Putting this altogether, the number of words is $$ 1 + 2\times \binom 62 + \binom 62\times \left[2 + \binom 42\right] + 32=183. $$

Answer 2

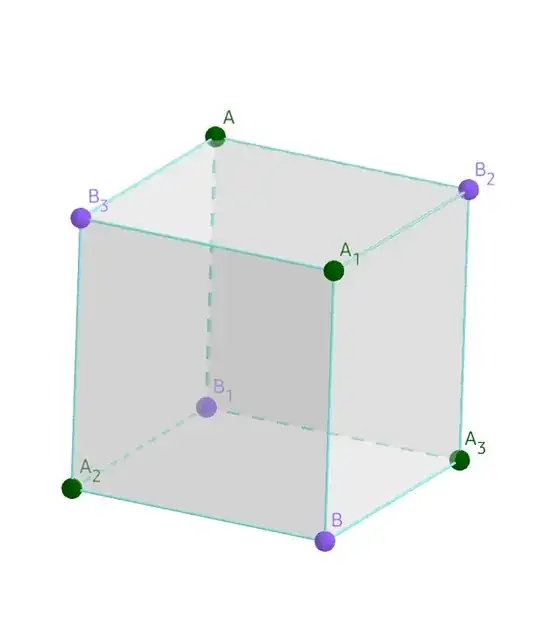
Consider the "adjacency matrix" of the cube, considered as an "undirected graph" :

$$A=\left(\begin{array}{cccccccc} 0&1&1&0&1&0&0&0\\ 1&0&0&1&0&1&0&0\\ 1&0&0&1&0&0&1&0\\ 0&1&1&0&0&0&0&1\\ 1&0&0&0&0&1&1&0\\ 0&1&0&0&1&0&0&1\\ 0&0&1&0&1&0&0&1\\ 0&0&0&1&0&1&1&0 \end{array}\right)$$

In every column of $A$, there are 3 "ones", accounting for the three neighbouring vertices for a certain ordering of the vertices of the cube. For example, in the first column, $A_{1,2}=A_{1,3}=A_{1,5}=1$ meaning that vertex $1$ has neighbouring vertices $2,3$ and $5$, etc.

The interest of this matrix is that the generic element $P_{i,j}$ of its k-th power $P:=A^k$ gives the number of different ways one can go from vertex $i$ to vertex $j$ in $k$ steps.

For example, consider :

$$A^2=\left(\begin{array}{cccccccc} 3&0&0&2&0&2&2&0\\ 0&3&2&0&2&0&0&2\\ 0&2&3&0&2&0&0&2\\ 2&0&0&3&0&2&2&0\\ 0&2&2&0&3&0&0&2\\ 2&0&0&2&0&3&2&0\\ 2&0&0&2&0&2&3&0\\ 0&2&2&0&2&0&0&3 \end{array}\right)$$

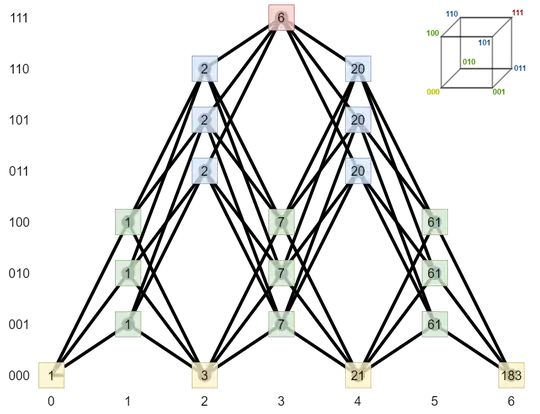
We indeed see that there are

• 3 ways to go from vertex 1 to itself in two steps (by going to one of its three neighbours then backtracking).

• 2 ways to go from vertex 1 to vertex 4 in two steps (indeed, they occupy two opposite vertices on a same face of the cube).

It now remains to consider, in $A^6$, the upper left entry which is $183$, somehow larger than the result you have found.

Matlab program :

clear all;close all;hold on;view(30,15);axis equal off;
V=[0,1,0,1,0,1,0,1
   0,0,1,1,0,0,1,1
   0,0,0,0,1,1,0,1];  % the 2^3=8 vertices of the cube
% generation of the upper part of matrix A :
A=zeros(8);
for p=1:8;
   for q=p+1:8;
      if (norm(V(:,q)-V(:,p))==1) 
         A(p,q)=1;Z=[V(:,[p,q])];
         plot3(Z(1,:),Z(2,:),Z(3,:),'linewidth',5,'b');
      end;
   end;
end;
A=A+A'; % taking symmetry of A into account
B=A^6;
B(1,1)
text(V(1,:)+0.05,V(2,:),V(3,:)+0.15, 
{'1','2','3','4','5','6','7','8'});

Answer 3

Another way: Imagine the cube is standing on its corner so that the vertices occupy four distinct heights, with the bead starting at the bottom vertex. The transition matrix for the height of the bead is

$$V=\left(\begin{array}{cccc} 0&3&0&0\\ 1&0&2&0\\ 0&2&0&1\\ 0&0&3&0 \end{array}\right)$$

and it's not too hard to calculate

$$V^6=(V^2)^3=\left(\begin{array}{cccc} 183&0&546&0\\ 0&547&0&182\\ 182&0&547&0\\ 0&546&0&183 \end{array}\right)$$

avoiding redundant calculations by noticing the symmetry. Relatedly, if you notice that the bead can only be at height $0$ or $2$ after an even number of steps, you can write the 2-step transition matrix for just these heights as

$$W=\left(\begin{array}{cc} 3&6\\ 2&7\\ \end{array}\right)$$

and then

$$W^3=\left(\begin{array}{cc} 183&546\\ 182&547 \end{array}\right).$$

Answer 4

Here's one more approach, using the principle of exclusion inclusion,

In the cube, mark the alternate vertices with green(denote this family of points by $A^*$) and purple($B^*$ ) colours as shown in the diagram. Note that for any move, the bead alternates between a $A^*$ and a $B^*$ in each move. Suppose the bead starts from the vertex $A$ and let the diagonally opposite vertex of $A$ be $B$.

Since, the bead alternates the $A^*$ and the $B^*$ for any possible move of the bead, it should be at a $B^*$ after its $5^{{th}}$ move. Note that all the $B^*$ except $B$ are adjacent to $A$, and hence it can reach $A$. So, we need to subtract the number of ways to reach $B$ from the total number of ways for the $5$ moves.

There are a total of $3$ paths to choose for the bead from each vertex and hence total of $3^5$ ways for the $5$ moves. And let $N$ be total such games which have been asked.

$$N=3^5-(\text{no. of ways to reach $B$ in $5$ moves})$$

After $4$ moves, the bead must be at $A^*$ and all the $A^*$ except $A$ are adjacent to $B$, and hence, it can move to $B$. So,

$$\text{No. of ways to reach $B$ in $5$ moves} = 3^4 - (\text{No. of ways to reach $A$ in $4$ moves})$$

Similarly arguing we get,

$$\text{No. of ways to reach A in $4$ moves} = 3^3 - (\text{No. of ways to reach $B$ in $3$ moves})$$

So we get,

$$N=3^5 - (3^4 - (3^3 - (3^2 - (3 - (\text{no. of ways to reach $B$ in $1$ move})))))$$

Since $A$ and $B$ are not adjacent and the bead starts from $A$, there is no way for the bead to reach $B$ in $1$ move.

$$N=3^5−3^4+3^3−3^2+3=183$$

Answer 5

Here's yet another approach. (It's not fundamentally different from Jean Marie's answer, but flattened and presented a little differently, so who knows, maybe it will be easier to follow for some people.) Divide the eight possible states of the bead into four classes, based on their distance from the starting state: $0, 1, 2, 3$. There is one $0$ state, three $1$ states, three $2$ states, and one $3$ state.

Let $a(t) = [a_k(t)]$ give the number of ways to get to a distance of $k$ after $t$ steps; we start with the array $a(0) = [1, 0, 0, 0]$.

Next, we need the dynamics. The only way to get to the $0$ state is to have come from a $1$ state at the previous stage; the same applies to getting to the $3$ state from a $2$ state. So

$$ a_0(t+1) = a_1(t) \qquad a_3(t+1) = a_2(t) $$

There are multiple ways to get to a $1$ state: You can to it from two of the three $2$ states—$2/3$ of them, in other words—or you can get to it from the only $0$ state. However, there are three $1$ states to tally up in all, so the recurrence is

$$ a_1(t+1) = 3\left[a_0(t)+\frac23 a_2(t)\right] = 3a_0(t)+2a_2(t) $$

and by symmetry

$$ a_2(t+1) = 3a_3(t)+2a_1(t) $$

We can now easily follow the progression of our system:

$$ a(0) = [1, 0, 0, 0] \\ a(1) = [0, 3, 0, 0] \\ a(2) = [3, 0, 6, 0] \\ a(3) = [0, 21, 0, 6] \\ a(4) = [21, 0, 60, 0] \\ a(5) = [0, 183, 0, 60] \\ a(6) = [183, 0, 546, 0] $$

so our answer is $a_0(6) = 183$. Note that the sums of the entries of $a(t)$ is $3^t$, which makes sense since there are $3$ ways to bead to move from any state.

Answer 6

Here is a nice visual solution to the problem. The number at any given vertex is the sum of the numbers associated to the vertices connected by incoming edges (i.e. the sum of all connected left neighbors). The numbers represent the number of $k$-step paths from $000$ to that vertex.