A polyhedron is a convex, three dimensional region bounded by a finite number of polygonal faces.
So is it possible that some of those polygonal faces be concave ? Can concave polygons be used in the process to form a 3D convex region ?
Asked
Active
Viewed 294 times
3
-
Excellent question! Mind posting some of your ideas first? – Ahaan S. Rungta Aug 20 '13 at 21:43
-
Since when did a polyhedron have to be convex? Most of the uniform polyhedra aren't: https://en.wikipedia.org/wiki/Uniform_polyhedron. – andybak Feb 11 '20 at 10:57
2 Answers
2
No. Every intersection of two convex shapes (such as a convex polyhedron and the plane through one of its faces) is convex.
Hagen von Eitzen
- 374,180
-
I can see how that is true intuitively but is there a name for this theorem? I'd be interested in looking up the proof. – andybak Feb 11 '20 at 10:58
2
If you allow two faces to be coplanar (which would be an unusual admission!), then
you could build a cube of six copies each of the triangle and nonconvex pentagon
shown left below.
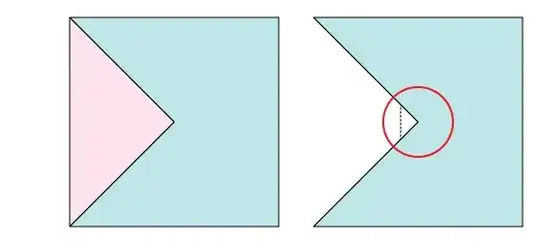
But if no two faces are coplanar, then in the neighborhood of a nonconvex point
on the boundary of a nonconvex face, there must be two points determining a segment
(dashed right above) with the segment exterior to the polyhedron. And this means
the polyhedron fails the definition of convexity, and so is itself nonconvex.
Joseph O'Rourke
- 30,327