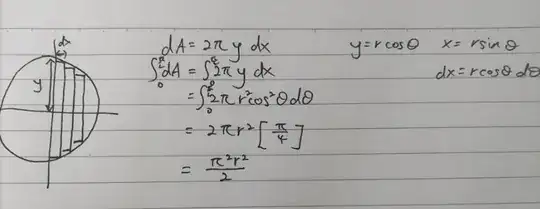I'm dividing the surface area to many small area that represent by formula $dA=2*\pi*y*dx$ but I cannot get the surface area which is $4\pi r^2$.
Can anyone point out where my mistake is ?
I would get $\pi^2 r^2$ as compare to $4\pi r^2$ , surface area is smaller than $4\pi r^2$ since value of pi is 3.142...
When you have the Perimeter of Circle $2 \pi y$ , you are multiplying by $dx$ , which is Parallel to $X$-Axis.
Likewise , you might multiply by $dy$ which is Parallel to $Y$-Axis.
Naturally , these 2 are wrong & will wrongly give the $\pi ^2$ :
We have to multiply by the Curve length $dS$ along the Circle.
$dS = \sqrt{dx^2+dy^2}$
Plug that in & then Check that you get Correct Surface Area.
$dA = (2 \pi y) dS$
Image Visualization :
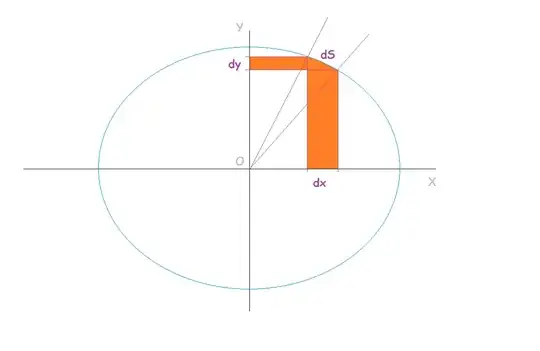
(1) Perimeter of Circle with Center on $X$-Axis is $2 \pi y$ , when we multiply that by $dx$ , Area is not along that Circle Curve.
(2) Alternately , Perimeter of Circle with Center on $Y$-Axis is $2 \pi x$ , when we multiply by $dy$ , Area is not along that Circle Curve.
(3) Correct way is to consider the Circle Curve , which has length $dS = \sqrt{dx^2+dy^2} = [\sqrt{1+(dy/dx)^2}]dx$ :
Then Area $dA = 2 \pi y dS$
Integrating this $dA$ with the limits will give the Necessary Surface Area.
You have the wrong formula for the area element. Assuming you're evaluating this area using a surface of revolution, you should have $$ dA = 2 \pi y(x) \sqrt{1 + \left(y'(x)\right)^2} \,dx$$ where $y(x) = \sqrt{r^2 - x^2}$. Then, the desired surface area is $$ SA = \int_{-r}^r 2 \pi y(x) \sqrt{1 + \left(y'(x)\right)^2} \,dx = 4\pi r^2$$ Basically, you're missing the factor of "$\sqrt{1 + \left(y'(x)\right)^2}$" that accounts for the curvature of the surface (and which doesn't appear when you're doing volumes of revolution). If you're curious about why this factor is there, check this link out.
You can simplify the above integral by using polar coordinates, which I see you tried to do in your work. That is, we have $$\begin{align} x &= r\cos(\theta)\\ y &= r\sin(\theta) \end{align}$$ where $r$ is fixed. Note that $$\frac{dy}{dx} = \frac{dy/d\theta}{dx/d\theta} = \frac{r\cos\theta}{-r\sin\theta} = -\cot\theta$$ Then, $$\begin{align} SA &= \int_{-r}^r 2 \pi y(x) \sqrt{1 + \left(y'(x)\right)^2} \,dx\\ &= -2\pi r^2 \int_{\pi}^0 \sin^2(\theta) \sqrt{1 + \cot^2(\theta)} \,d\theta\\ &= 2\pi r^2 \int_0^\pi \sin\theta \,d\theta\\ &= 4\pi r^2 \end{align}$$ as desired.
In the realm of multivariable calculus, one would perform this integral using spherical coordinates. Here, the the area element would be $$ dA = r^2 \sin\theta \,d\theta d\varphi$$ where $\theta$ is now the polar angle, and $\varphi$ is the azimuthal angle. The the surface area is then simply given by $$ SA = \int_{0}^{2\pi} \int_0^{\pi} r^2 \sin\theta \,d\theta d\varphi = 4\pi r^2 $$
