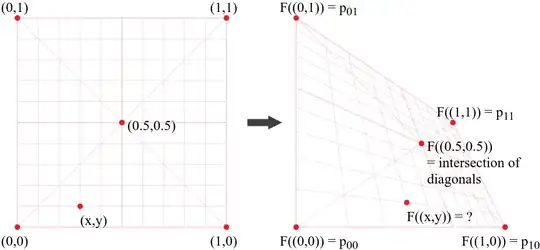
Suppose we know that $F:\mathbb{R}^2 \to \mathbb{R}^2$ is a perspective warp function; that is, there exist real parameters $a,b,c,d,e,f,g,h,i$ such that, for all $(x,y)$: $$ F((x,y)) = ((ax + by + c), (dx + ey + f)) / (gx + hy + i). $$ And suppose we are not given $a,...,i$, but instead we are given the values of F on the corners of the square: $$ F((0,0)) = p_{00} \\ F((1,0)) = p_{10} \\ F((0,1)) = p_{10} \\ F((1,1)) = p_{11} $$ And assume $p_{00},p_{10},p_{11},p_{01}$ form a convex quadrilateral.
Can we then evaluate $F((x,y))$ for an arbitrary input point $(x,y)$?
One way to do it is to solve for the 9 parameters $a,...,i$, and then evaluate the resulting explicit formula for $F$ at the desired $(x,y)$. There are actually only 8 degrees of freedom in $F$, since any scalar multiple of a given solution $a,...,i$ is also a solution representing the same $F$; and there 8 scalar equations, so this is a well-constrained system of equations.
Finding the Transform matrix from 4 projected points (with Javascript) shows another method for computing the parameters of $F$.
But is there a more neat and direct geometric method for evaluating $F$ in terms of the sample points $p_{00},p_{10},p_{01},p_{11}$?
Here are a couple of observations that give us the answer easily in some special cases.
Observation #1: Since $F$ preserves straight lines, $F((0.5, 0.5))$ must be the intersection of the two diagonals: $$ F((0.5, 0.5)) = \frac{\mathrm{Area}(p_{00},p_{10},p_{01})p_{11} + \mathrm{Area}(p_{11},p_{01},p_{10})p_{00}} {\mathrm{Area}(p_{00},p_{10},p_{11},p_{01})} $$
Observation #2: If $p_{00},p_{10},p_{11},p_{01}$ happen to form a parallelogram, then $F$ is an affine warp, in which case we can evaluate F at any $(x,y)$ by using bilinear interpolation: $$ F((x,y)) = (1-x)(1-y)p_{00} + x(1-y)p_{10} + (1-x)y \; p_{01} + x \; y \; p_{11} $$
In general, I expect the answer will be a neat symmetric-looking formula having the flavor of the above two special cases: that is, an affine combination of the points $p_{00},p_{10},p_{01},p_{11}$, with the coefficients being some expressions involving $x$, $y$, and possibly triangle areas or cross ratios involving the four points. In particular, when $x,y \in [0,1]$, I expect the formula will naturally be a convex combination of the four points.