1

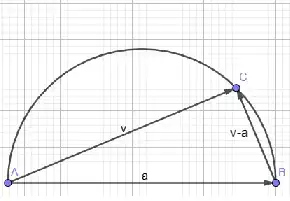
Fix $a$ in $\mathbb R^2$. What is the locus of points $\{v : v \in \mathbb R^2$ and $v \cdot (v-a) = 0\}$?

Clearly, $0$ and $a$ are in this set, and no other multiple of $a$ is in the set. Beyond that, I'm having trouble characterizing it.

Update

Let $a = (p, q)$. Then:

$$x^2 + y^2 - px - qy = 0\\ (x - \frac{p}{2})^2 + (y - \frac{q}{2})^2 = r^2$$ where $r = \frac {\sqrt {p^2 + q^2}} 2.$ That is, a circle with center $a/2$ and radius $\|a\|/2$. Wow.

This obviously implies that $$(v−a/2)⋅(v−a/2)=a/2⋅a/2$$ defines the same circle, which makes sense, because the equation is stating: Take $v$, shift it by $a/2$, and its length squared must equal a constant (namely the length of $a/2$ squared).

I'm still struggling to "see" this in the original equation $v \cdot (v-2b) = 0$. Does it mean that the locus of points, that when translated by a constant have vectors orthogonal to the midpoint of the translation vector, is a circle? I can't (yet) see that geometrically.

Update

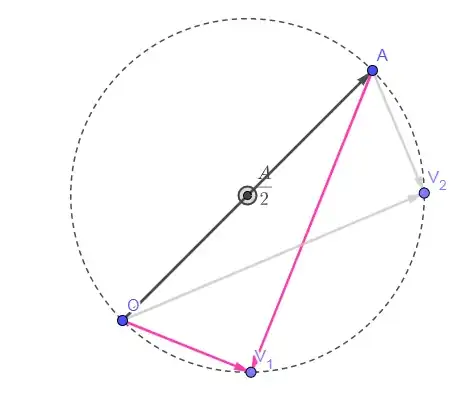
It's Thales' Theorem: If $a/2$ is the center, then $OA$ is a diameter, and $OV \perp AV$ for any $V$ on the circle: enter image description here

Or, to put it differently: For any two distinct points $O, A$, a circle is the locus of points $V$ such that $OV \perp AV$. Then $OA$ is a diameter and $A/2$ the center.

Narasimham
  • 40,495
SRobertJames
  • 4,278
  • 1
  • 11
  • 27
  • 2
    write $v=(x,y) $ and $a = (a_1, a_2) $ and calculate. Completing squares is involved – Will Jagy Jun 19 '23 at 01:29
  • Maybe it is a cycle in $\mathbb{R}^2$. – fusheng Jun 19 '23 at 01:36
  • 2
    @WillJagy No need to use coordinates: $v\cdot(v-a) =0$, then $ (v-a/2)\cdot(v-a/2) = a/2\cdot a/2$. – jjagmath Jun 19 '23 at 03:50
  • @jjagmath sure. I was hoping that supplying a framework that would seem more familiar would induce the OP to give it a try, I guess that did not happen. I also liked the bit about inscribed triangles with one edge a diameter – Will Jagy Jun 19 '23 at 16:52
  • Robert, how about if you type the equation (with $x,y,a_1, a_2$ ) at the end of your equation to begin with – Will Jagy Jun 19 '23 at 19:07
  • @WillJagy Got it! Thanks! Please take a look. Also: What type of course or text covers these multivariate algebra cases? It seems to be a gap in my skills, but I can't find a good reference, source, or method. – SRobertJames Jun 19 '23 at 19:25
  • 1
    fine. Note that you were able to fill in the steps above, after which you were able to write things as vectors; keep practicing one-variable algebra, don't be too quick to tell us you can't use our hints. On this problem: there is a triangle with vertices $0, a, v.$ How does it fit in the circle, and what kind of triangle is it? For example, take $a = (6,8)$ Where is the circle center? Can you find some other points on the circle with integer coordinates $v=(x,y)?$ Helps to draw an actual picture. There is a geometry theorem illustrated here... – Will Jagy Jun 19 '23 at 19:37
  • @WillJagy Thales Theorem! Updated accordingly. – SRobertJames Jun 19 '23 at 20:12

1 Answers1

1

You have answered your own question.

$0$ as a null vector does not occur here. It occurs as a scalar dot product.

The dot product is the statement of Thales thm in vector form. Vectors $(v,v-a)$ are orthogonal and the locus is a semi-circle containing all right angled triangle vertices. Only a single case is drawn.

enter image description here

Narasimham
  • 40,495