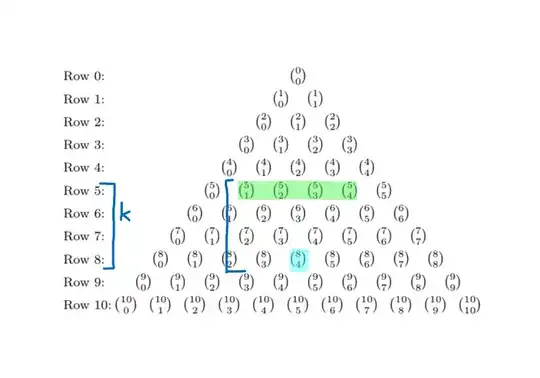
In a standard Pascal's triangle, the entry in the $n$th row and $r$th column denoted as ${n \choose r}$ can be expressed using $k+1$ entries $k$ rows above itself as $${n \choose r}=\sum_{i=0}^k {k \choose i}{n-k \choose r-k+i}$$ where $0\le k\le r$.
A simple example to help visualize the identity: