Here are some hints.
Proving well-definedness
Before we can start thinking about injectivity and surjectivity, we should first prove that this function is well-defined. That is, given natural numbers $x$ and $y$, we should check that $f(\langle x,y \rangle)$ is in fact a natural number. The $\frac{1}{2}$ that appears in the definition of $f$ is alarming. In order for $f(\langle x,y \rangle)$ to be a natural number, we need $(x+y)^2 + 3x +y$ to be an even natural number. Why is this the case?
Basic algebra is not enough to prove bijectivity
The tricky thing about this function is that it is not injective when regarded as a function $f: \mathbb{R} \times \mathbb{R} \to \mathbb{R}$. (For example, we have $f(\langle 0, 1 \rangle) = 1 = f(\langle \frac{-3 + \sqrt{17}}{2}, 0 \rangle).$)
So, at least for proving injectivity, we will have to resort to some combinatorial or number theoretic property of the natural numbers—basic algebraic manipulations will not be enough.
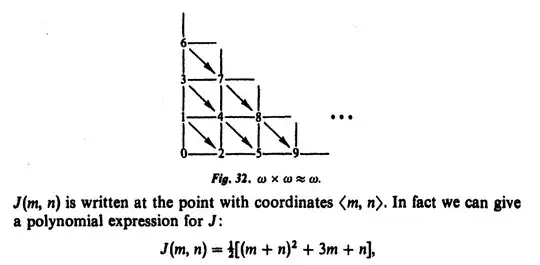
Using the picture
It is clear that the function shown in the picture is bijective. So, if we can show that $f$ is the function shown in the picture, we will be done.
First, we observe that the function shown in the picture is $\langle x,y \rangle \mapsto T_{x+y} + (x+1) - 1$, where $T_n$ denotes the $n$th triangular number. This is true because the points enumerated by $f(\langle 0, 0 \rangle), f(\langle 0, 1 \rangle) , f(\langle 1, 0 \rangle), f(\langle 0, 2 \rangle) \dots, f(\langle x,y \rangle)$ form a triangle of side length $x+y$ plus a row of length $x+1$ and because the enumeration starts at $0$.
There is a nice formula for the triangular numbers that can be obtained by induction. Once you have obtained this formula, you can use simple algebra to show that $f(\langle x,y \rangle) = T_{x+y+1} + (x+1) - 1$.