Are there any Mathematical Theorems that Can Prove the Results of this Experiment?

Question

I had the following question about Probability and Estimation.

Let $\hat{\theta}_n$ be an estimator of a parameter $\theta$ based on a random sample of size $n$. The estimator $\hat{\theta}_n$ is said to be Consistent if, for any positive value $\epsilon$, the following condition holds as $n$ approaches infinity:

$$\lim_{{n \to \infty}} P(|\hat{\theta}_n - \theta| < \epsilon) = 1$$

In other words, for any small value $\epsilon$, the probability that the estimator $\hat{\theta}_n$ deviates from the true value $\theta$ by more than $\epsilon$ tends to zero as the sample size increases.

My Question: Recently, I have been thinking about the following question related to the above: Is it possible that the variance of an estimator also reduces as the sample size increases?

$$\lim_{{n \to \infty}} \text{var}(\hat{\theta}) = 0$$

I tried to find a mathematical theorem to support the above idea but I could not find a theorem that precisely described this idea (variance decreases as sample size increases) - the closest thing I could find was the Law of Large Numbers: The average of the results obtained from a large number of trials should be close to the expected value and will tend to become closer to the expected value as more trials are performed:

The strong law states that with probability 1, the sample mean $\bar{X}_n$ converges to the expected value $E[X]$ almost surely as $n$ goes to infinity: $$\lim_{n \to \infty} \bar{X}_n = E[X] \quad \text{almost surely}$$

Intutively, I interpret this as follows: Suppose I am repeatedly throwing darts at a board - now imagine that the more darts I throw, I start to fall into a routine and reach a certain level of consistency. All my darts will begin to cluster in smaller and smaller areas as time goes on, and thereby the more darts I throw (i.e. larger sample size) - it is not unreasonable to expect that I will observe lesser variability (i.e. lesser variance) on average. However, I am not sure if this analogy can be used to study my idea of the relationship between "decreasing variance and increasing sample size".

To test this idea, I tried to perform the following experiment using the R programming language: For a Normal Distribution with (10,10) - random samples for different sizes are taken and the sample mean, sample variance, variance of the sample mean and variance of the sample variance are calculated. This process is then repeated many times.

Here is the corresponding R code:

library(dplyr)
results_df <- data.frame(i = numeric(), j = numeric(), sample_size = numeric(),
                         sample_mean = numeric(), sample_variance = numeric(),
                         sample_variance_of_mean = numeric(), sample_variance_of_variance = numeric())
for (i in 2:1000) {
for (j in 1:100) {
sample &lt;- rnorm(i, 10, 10)


sample_mean &lt;- mean(sample)


sample_variance &lt;- var(sample)


sample_sd &lt;- sqrt(sample_variance)
#print(i)

sample_variance_of_mean &lt;- sample_variance / i


sample_variance_of_variance &lt;- (2 * sample_sd^4) / (i - 1)


results_df &lt;- rbind(results_df, data.frame(i = i, j = j, sample_size = i,
                                           sample_mean = sample_mean, sample_variance = sample_variance,
                                           sample_variance_of_mean = sample_variance_of_mean,
                                           sample_variance_of_variance = sample_variance_of_variance))

}
}
summary_stats <- results_df %>%
  group_by(sample_size) %>%
  summarise(mean_sample_mean = mean(sample_mean),
            mean_sample_variance = mean(sample_variance),
            mean_sample_variance_of_mean = mean(sample_variance_of_mean),
            mean_sample_variance_of_variance = log(mean(sample_variance_of_variance)))
graph <- ggplot(summary_stats, aes(x = sample_size)) +
    geom_point(aes(y = mean_sample_mean, color = "Average Mean")) +
    geom_line(aes(y = mean_sample_mean, color = "Average Mean")) +
    geom_point(aes(y = mean_sample_variance, color = "Average Variance")) +
    geom_line(aes(y = mean_sample_variance, color = "Average Variance")) +
    geom_point(aes(y = mean_sample_variance_of_mean, color = "Average Variance of Sample Mean")) +
    geom_line(aes(y = mean_sample_variance_of_mean, color = "Average Variance of Sample Mean")) +
    geom_point(aes(y = mean_sample_variance_of_variance, color = "(Log) Average Variance of Sample Variance")) +
    geom_line(aes(y = mean_sample_variance_of_variance, color = "(Log) Average Variance of Sample Variance")) +
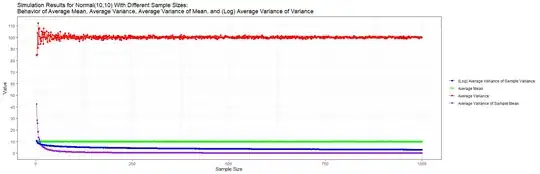
    labs(title = "Simulation Results for Normal(10,10) With Different Sample Sizes:\nBehavior of Average Mean, Average Variance, Average Variance of Mean,\nand (Log) Average Variance of Variance",
         x = "Sample Size", y = "Value") +
    scale_color_manual(name = "", values = c("blue", "green", "red", "purple")) +
    theme_bw() +
    scale_y_continuous(breaks = seq(0, 110, 10))
graph

Based on this graph, we can see that:

• The sample mean and the sample variance move closer and closer to their true values as the sample size increases. This is to be expected based on the "Consistency" properties of MLE (Maximum Likelihood) estimators
• The variance of the sample mean and the variance of the sample variance move closer and closer to $0$ as the sample size increases - - thus for this specific experiment, validating the initial idea that I had regarding the relationship between decreasing variance with increasing sample sizes
• The variance of the sample mean appears to move towards $0$ at a faster rate compared to the variance of the sample variance ... I wonder if there is a reason for this?
• A final observation, although the sample variance does move towards its true value as the sample size increases - it seems to "bounce around" more compared to the other estimators ...I wonder if there is a reason for this?

But in general, Are there any theorems in probability that formally validate the results of this experiment and the initial idea that I had?

Thanks!

References: Variance of Sample Variance

• Notes: Formulas from question - given some observed data $X_i : x_1, x_2...x_n$ where $X \sim \mathcal{N}(\mu, \sigma)$:

• 1. Sample Mean: $\bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i$
• 2. Sample Variance: $s^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2$
• 3. Variance of Sample Mean: $\text{Var}(\bar{x}) = \frac{s^2}{n}$
• 4. Variance of Sample Variance: $\text{Var}(s^2) = \frac{2 \cdot s^4}{n-1}$

Answer 1

A consistent estimator implies the convergence in probability to a constant. But that does not imply that the variance will go down to $0$, or $L^2$ convergence. Consider this popular example- $$ \hat{\theta}_n = \begin{cases} \theta ~~\text{with probability $\frac{n-1}{n}$}\\ \theta+n ~~ \text{with probability $\frac1n$} \end{cases} $$ then we have convergence in probability, but also $E(\hat{\theta}_n-\theta)^2 = 0\cdot \frac{n-1}{n} + n^2\cdot \frac1n=n \rightarrow \infty$ hence it's variance is not finite, which demonstrates the above.

$L^q$ convergence is a stronger notion of convergence and to check this we generally use the notions of uniform integrability and almost sure convergence. This tells us that if we have almost sure convergence and finite variance, then uniform integrability (of say order $q$) of a sequence of random variables is the same as the $L^q$ convergence and vice versa.