2

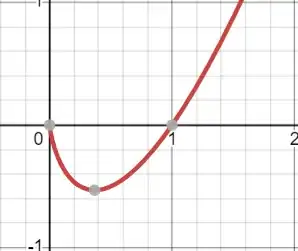
I can understand it algebraically, but I wanted some geometric-esq intuition for why the graph is this way. Like some intuition that I could've used to derive it.

This is the plot:

I eked out some explanation for what's happening (not sure how correct it is):

A log:

enter image description here

We want it to swoop back in to zero instead of going to -infinity though. So, we weight it by $x$ (which gets smaller as it goes to $- \infty$

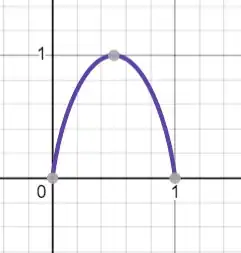
enter image description here

Flip it

enter image description here

Now copy it, flip horizontally, and push it to 1 (since we want the graph to be from 0 to 1).

enter image description here

My brain is happy with everything above, what it isn't happy with is that when I add both of them together: the part in the middle gets added as expected but the parts at the ends just go away? What witchcraft is this?

enter image description here

proof-of-correctness
  • 420

1 Answers1

3

You can add them only in the part where they are both defined. The red function is not defined for $x<0$ and the blue one is not defined for $x>1$, so the common domain is $[0,1]$.

By the way, this is a rather interesting functions called the Binary entropy function.
It has many important properties, and defines the entropy (uncertainty) of a coin flip with $\mathbb{P}(\text{coin falls on head})=x$.

Kolja
  • 2,760
  • ohh okay! thank you so much! btw, what kinds of interesting properties does it havee? – proof-of-correctness Jun 02 '23 at 18:27
  • I suggest reading this Wikipedia article. The entropy function can be generalised to probability events with larger sample spaces. For example, a loaded dice with probabilities $p_1,\ldots, p_1$ has entropy $\sum p_i \log(\frac{1}{p_i})$, or more generally for a random variable $X$ we have $H(x)=\mathbb{E}[-\log{X}]$. Given two random variables $X$ and $Y$, we can define the distance between them as $D_{KL}(X||Y)=\sum P(x) \log(\frac{P(x)}{Q(x)})$, and this distnace satisfies all required properties. – Kolja Jun 05 '23 at 06:48
  • Furthermore the entropy always attains its maximum at the uniform distribution (informally that is the "most unpredictable distribution").
    Another nice property, suppose you have a set of cardinality $n$, and you want to know how many subsets of cardinality $k$ are there, with $p=\frac{k}{n}$. We know this is ${n \choose k}$, but we can also give a nice asymptotic approximation with $2^{n H(p)}$, or even some bounds as shown here.     – Kolja Jun 05 '23 at 06:53