Can this simple diagram of a triangle and three circles be constructed with straightedge and compass?

Question

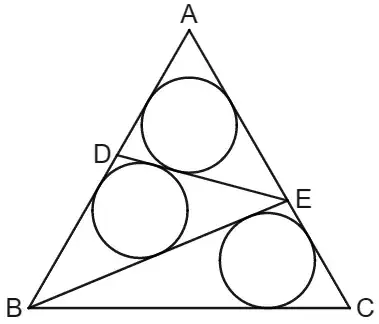
Here is a diagram from a question that I asked recently.

In equilateral $\triangle ABC$, $D$ is on $AB$, and $E$ is on $AC$. In the three regions thus formed, circles of equal radii are inscribed.

Can this diagram be constructed with straightedge and compass?

If we construct the chords, then the circles are easy to draw.

Assuming that $AB=1$, the closed form expressions of the lengths and angles are not simple, so I wouldn't be surprised if the diagram cannot be constructed with straightedge and compass.

radius of circles $=r=\frac{\sqrt{3}}{30}\left(7-\sqrt[3]{2}-2\sqrt[3]{4}\right)=0.148\ldots$

$BD=DE=\sqrt{\dfrac{3 (651+392\sqrt[3]{2}-436\sqrt[3]{4})}{50(-94-23\sqrt[3]{2}+134\sqrt[3]{4})}}=0.550\ldots$

$EC=\dfrac{1}{1+2^{2/3}}=0.386\ldots$

$\angle{DBE}=\arccos{(2^{-1/3})}=37.467\ldots^{\text{o}}$

On the other hand, the essence of the diagram is very simple (the diagram can be precisely described in just a few words, as I did at the beginning of my question). And, earlier I asked about another construction involving four circles and two chords, and the answer turned out to be much simpler than I expected (although still quite clever). So I still have a sliver of hope that my diagram here can be constructed somehow.

Answer 1

To expand my comment into a proper answer: your diagram cannot be constructed via compass and straightedge. The main problem is the $2^{1/3}$ in your calculations; it corresponds to the minimal polynomial $p(x)=x^3-2=0$ over the rational numbers. The field extension required to be able solve this in terms of elements of $\mathbb{Q}$ is therefore $3$.

Now consider compass and straightedge construction in more detail. There are two operations you can do: draw a line containing two previously defined points, or draw a circle centred at one previously defined point and passing through another. Any new points are a result of the intersection of these elements. Some basic Cartesian geometry will show that these new points satisfy at most a quadratic equation with coefficients in terms of previously constructed lengths (or the rationals themselves). In other words, any constructed length that is not rational represents a field extension of degree 1 or 2. Since constructed lengths are built upon one another, the tower rule says that the degree of the field extension represented by any one of them is the product of the extension degrees of the constructions that one is built from. As these all can only be 1 or 2, the degree of the field extension it represents is a power of 2.

And now we see the contradiction. To construct a length of $2^{1/3}$ would require a field extension of degree $3$, but constructible points can only ever have field extensions whose degree is a power of $2$. But there is no power of $2$ that is equal to $3$, so your diagram is not constructible.

Answer 2

You can't docthe straightedge and compasses construction with an equilateral triangle, but a $30°-60°-90°$ right triangle offers an easy solution. Simply bisect the $60°$ angle, then bisect the $120°$ angle formed where the first angle bisector meets the opposite leg. The three component triangles so formed are all congruent and thus so are their incircles.