Assume that $D\subseteq \mathbb R^2$ is a closed disc and $S$ is its boundary circle. Moreover $x,y\in S$ are distinct points, which determine exactly two arcs $I,J\subseteq S$, and $f:D\rightarrow \mathbb R$ is a continuous function such that $f(x)<0$, $f(y)>0$.
I want to prove the following:
There exist points $p\in I$, $q\in J$ and a connected set $C\subseteq f^{-1}(0)$ such that $p,q\in C$.
To me it seems intuitively true, but I have no serious idea how to prove it. Any help appreciated!
Here is an idea for a construction:
This reminds me of the game hex https://en.wikipedia.org/wiki/Hex_(board_game) and the proof that there is always a winner.
There does not seem to be anything special about the structure of the disk in your problem, so we could think of it as a hex board, with $x$ and $y$ being on opposite sides. Further assume:
If $f$ is has a zero on a hexagon, mark it red, otherwise blue.
If there were a path of blue hexagons from left to right, we would have a contradiction by the intermediate value theorem. So there must be a path of red hexagons from top to bottom.
Of course this does not give a continuous path, but I suspect that by refining the grid, we could construct a path (or at least a connected set) in the limit.
Strategy: I'll do a proof by contradiction, assuming that $f^{-1}(0)$ has no connected component $\Gamma$ that intersect's $I$ and $J$. In this setting i'll construct a continuous curve that connect two points $P_1,P_2$ s.t. $f(P_1)>0, f(P_2)<0$ and the contradiction will follows by the Intermediate value theorem.
Setting: The decomposition in connected components of $f^{-1}(0)$ is:
$$ f^{-1}(0)=\bigcup_\alpha A_\alpha \cup\bigcup_\beta B_\beta \cup\bigcup_\gamma C_\gamma,\;\; \text{ where: } $$ $$A_\alpha\cap I\neq \emptyset,\;\; B_\beta\cap J\neq \emptyset,\;\;C_\gamma\cap I=C_\gamma\cap J= \emptyset, $$ Lets define $A=\bigcup_\alpha A_\alpha,\;\; B=\bigcup_\beta B_\beta$.
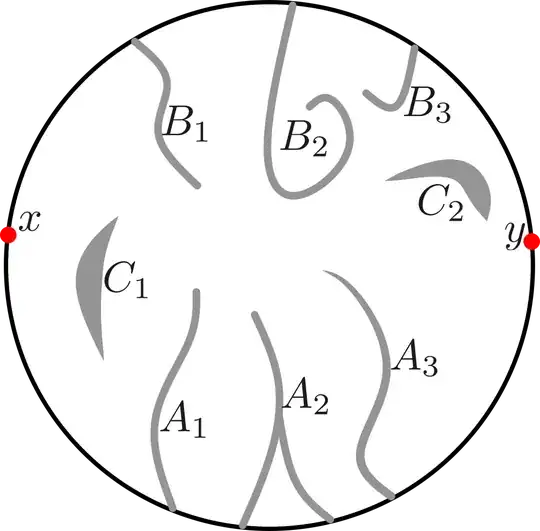
Because i want work with the open set of $\mathbb R^2$, lets call $x',y'$ two point inside in disc near to $x$ and $y$ s.t. $f(x')>0,f(y')<0.$
$A$ enlargement: In this part I want expand $A$ to have a nicer boundary that will be useful in the next part, in the same time i want to preserve some of his property (does not intersect $x,x',y,y',I,B,C$ and the compactness ). $$\varepsilon:=\frac{1}{3}\min \{d(A,x),d(A,x'),d(A,y),d(A,y'),d(A,I),d(A,B),d(A,C)\}, $$ and now I extract a finite open covering from the trivial covering with the $\varepsilon-$balls: $$A\subset \bigcup_{i=1}^N B(k_i,\varepsilon)\subset \overline{\bigcup_{i=1}^N B(k_i,\varepsilon)} =A_\varepsilon. $$
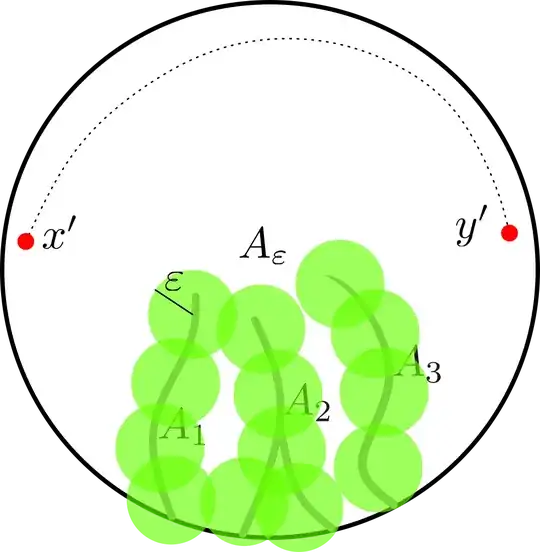
Study of set $D\backslash A_\varepsilon$: Now we'r studying topological property of the connected component of $\stackrel{\circ}{D}\backslash A_\varepsilon$ that contains $x'$, lets call $X$ that open set. Because $A_\varepsilon$ its compact that doesn't intersect the compact $I$, there is a distance $d>0$ between this two disjoint set, so we can construct a path $\gamma$ (near to $I$, inside $X$) that link the two points $x',y'\implies y'\in X$.
Now observes that $X^c\subset \mathbb R^2$ (its only the union of $D^c,S^1,A$ and the other connected component of $\stackrel{\circ}{D}\backslash A$ that have the boundaries in $A_\varepsilon\cup S^1 $) its connected, and by this we get that $X$ is simply connected (we used the fact that $S^1\cap A_\varepsilon\neq \emptyset$). So $X\subset \mathbb R^2$ is a non-empty, open subset of $\mathbb R^2$, simply-connected, hence by the Riemann mapping theorem its biholomorphic to the open unit disc: $$\phi:X\to \stackrel{\circ}{D}.$$ Now by construction, the $X$'s boundary is regular enough (remember that $X$ is one component of $\stackrel{\circ}{D}\backslash \{\text{finite balls}\}$) to satisfy the $3.$ property of Cecchi's answer, hence we can extend $\phi$ to the closure (and it is still an homeomorphism): $$\phi:\overline X\to D $$
Study of set $X\backslash B$: Now $\phi(x)$ and $\phi(y)$ goes to the boundary and define two arc (like before) $I',J'$ and by continuity (wlog) $\phi(I)=I'$. $\phi(B)$ is compact and intersect $I'$ and its disjoint from $J'$ so there exists (like before) a path $\gamma'(t)$ near to $J'$ that links $\phi(x)$ to $\phi(y)$ disjoint from $\phi(B)$, more we can request that $\gamma'(t)$ is disjoint from $\phi(C)$ (it is compact and disjoint from $J'$ too). Finally we get a path $\gamma(t)=\phi^{-1}\circ\gamma'(t)$ in $X$ disjoint from $B$ and $C$, hence a path in $D$ disjoint from $A$,$B$ and $C$ that links $x$ to $y$.
Contradiction : Now we get a contradiction because $f\circ \phi(t)$ is never zero (the support of $\phi$ doesn't intersect $f^{-1}(0)=A\cup B\cup C$) and is a continuous map that start positive and ends negative.
