0

Does the Wave Equation (and other PDEs) define an ODE if I took the behavior in 1D of just one point in space? How I find the ODE from the PDE eqn.?

Intro______________

Since is a conceptual question, I am not really sure how to describe it, so I am going to use an example to explain what I want to ask.

Lets think in a classical PDE as it is the 1D wave equation: $$\frac{\partial^2 F(x,t)}{\partial x^2}-\frac{1}{c^2}\frac{\partial^2 F(x,t)}{\partial t^2} = 0 \label{Eq. 1}\tag{Eq. 1}$$ where as usual "$c$" is the constant speed at which the traveling solutions move: $$F(x,t) = f(x-ct)+g(x+ct)\label{Eq. 2}\tag{Eq. 2}$$ with these functions $f$ and $g$ been dependent of the border conditions of the problem.

Let think now in a particular solution to the wave equation: for making it simple I will choose to have $c=1$ so the wave equation becomes $$F_{xx}-F_{tt}=0\label{Eq. 3}\tag{Eq. 3}$$ and a particular solution through a smooth bump function: $$F(x,t) = \begin{cases} \displaystyle{\exp\left(-\frac{1}{1-(x-t)^2}\right)},\quad(x-t)^2<1 \\ \qquad\qquad 0\qquad\qquad\!\quad,\quad (x-t)^2\geq 1 \end{cases}\label{Eq. 4}\tag{Eq. 4}$$ where you can check it is indeed a solution to \eqref{Eq. 3} since the trivial zero solution solves the PDE outside $(x-t)^2\geq 1$, and inside you could check it here in Wolfram-Alpha. I took this solution from a more general form shown this amazing answer by @NinadMunshi, but you can also review the form of \eqref{Eq. 4} in Wolfram-Alpha.

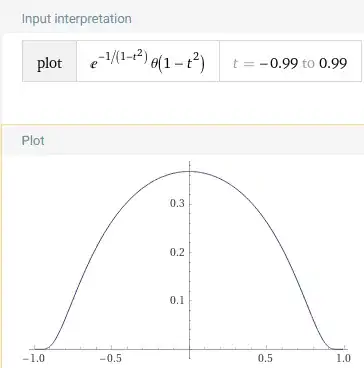
Now, if I want to focus in the behavior only in one point in space $x = x_0$, for ease lets say at $x_0 = 0$, then the behavior in time of $F(x,t)$ at $x=0$ will be given by the function: $$y(t) = F(0,t) = \begin{cases} e^{-\textstyle{\frac{1}{1-t^2}}},\quad t^2<1 \\ \quad 0\quad\;,\quad t^2\geq 1 \end{cases}\label{Eq. 5}\tag{Eq. 5} $$ which bell-like shape can be reviewed here.

eqn 5

Now, from \eqref{Eq. 5} you can check here that $y(t)$ follows this non-linear ODE: $$y'(t) +\frac{2t}{(1-t^2)^2}y(t) = 0 \label{Eq. 6}\tag{Eq. 6}$$

So it can be seen that for PDE like the Wave Equation under some boundaries conditions which define a specific solution, this solution defines in an specific point in space and focusing only in one coordinate axis an ODE which the solution also must fulfill.

But since PDEs got non-unique solutions in general, and ODE are much more restricted in this sense, I am not sure if always is possible to find an ODE neither how to get it from the PDEs general solutions, if it is possible.

So for a general PDE with some boundary conditions defined by some function $h(\partial \Omega)|_{t_0}$ in some boundary $\partial \Omega$, I believe there should be some constraints over the function $h(\partial \Omega)$ behavior such it could be a solution to the PDE, which should in principle restrict somehow the ODE that both equations will define at some point in space as time passes.

Main Question______

  1. It is possible to obtain an ODE for a specific point in space within one of the coordinate axis from a general solution form of a PDE? How it is obtained? Defined border conditions are always required?
  2. If it is not possible in general, It is possible for the Wave Equation which general solution form is known as traveling waves $Y(\vec{k}\cdot\vec{x}-ct)$? If not in general, It is possible for the plane waves' decomposition of a general solution?
  3. If is still not possible, Could be done in general for the 1D Wave Equation? How?

So far I tried for the 1D wave equation example unsuccessfully: If I just make the term $\frac{\partial^2 F(x,t)}{\partial x^2}\Biggr|_{x_0}=\alpha$ a constant I just end with a 2nd order polynomial in time, and I also tried to put a solution of the form $F(x,t)=\delta(x-x_0)U(x_0,t)$ in \eqref{Eq. 1} but only found "non-senses".

Joako
  • 1,380
  • If such an ODE does exist, it cannot be first order, as if $y(0) = y_0$, $y$ could either increase or decrease depending on whther a wave is traveling left or right as it crosses $x=0$. Since solutions of ODEs are unique, a first-order ODE cannot describe both of these behaviors. – whpowell96 May 30 '23 at 02:51
  • This may be easier to consider for an edvection equation, $u_t + au_x = 0$ to start since that is first order – whpowell96 May 30 '23 at 02:52
  • @whpowell96 There are first order ODEs which are non-linear and could have singular solutions where more than one behavior is possible, as example $y'=\text{sgn}(y)\sqrt{|y|},\quad y(0)=0$ could have as solutions $y(t)=0$, $y(t)=\frac{t^2}{4}$, and $y(t)=-\frac{t^2}{4}$, don't meaning here it solve the problem I am asking for, but shows that first order ODEs could do these kind of "weird things" – Joako May 30 '23 at 03:35
  • @whpowell96 About your second comment, it could be true. I started from the wave equation since I have much more familiarity with it (I did research a decade ago on laser light when studying engineering). But I am rusty AF. – Joako May 30 '23 at 03:37
  • Yes, but your proposed ODE should have a unique solution, as it is a projection of a PDE with a unique solution. The behavior you mention cannot happen in a regime where solutions are unique. Another way to see it is that the wave equation is actually system of PDEs for $F$ and $F_t$, which is why you need two initial conditions for it. This behavior should be reflected in your ODE as well. – whpowell96 May 30 '23 at 03:39
  • @whpowell96 Could you elaborate in an answer in what you mean with "the wave equation is actually system of PDEs"? part of the problem why I am asking this question is because I am a bit confused in what really mean a PDE: I always though about it as multi-variable ODEs but now I figure out there are a complete different kind of "monster", it is different asking what it is $\frac{\partial}{\partial t} u(x,t)$ from $\frac{\partial}{\partial t} u(x(t),t)$ and from $\frac{\partial}{\partial t} u(x(t))$, and now I have a mess in my brain. – Joako May 30 '23 at 03:57
  • 2
    Let $F = u$ and $v = u_t$, then $u_{tt} -c^2u_{xx} = 0$ is equivalent to the system $u_t = v$, $v_t = c^2 u_{xx}$ – whpowell96 May 30 '23 at 04:00
  • @whpowell96 now I am even more confused: if I take 2nd time derivatives to $$\frac{\partial^2}{\partial t^2}u(x,t) = u_{tt}$$ which should be something completely different from $$\frac{\partial^2}{\partial t^2}u(x(t)) = \frac{\partial^2}{\partial x^2}u(x(t))\cdot(x')^2+\frac{\partial}{\partial x}u(x(t))\cdot x''$$, but if I forced them to be equal (don't fully understanding what restricitions I am impossing), if I set a constant speed $x'=c\Rightarrow x''=0$ suddenly I got for "coincidence" a wave equation $$u_{tt}=\frac{\partial^2}{\partial x^2}u\cdot c^2$$.... I have a conceptual mess :( – Joako May 30 '23 at 05:15
  • 1
    $x$ is independent from $t$ – whpowell96 May 30 '23 at 05:45

0 Answers0