Note
After reading Dunham's answer once more, I realized he pointed out a critical mistake you've made directly (which I had done here also indirectly). In the bulk of this answer, I will from scratch, explain how Taylor series ist just nested linear approximations.
You need to increase the number of sample points to involve higher derivatives!
Taylor series is one of my favourite topics in mathematics, and I have gone through this same question you have myself before. The issue is of how you incoporated the second derivative. (Step-5)
We will first talk about approximating functions discrete sampling, and then talk about what happens when the sampling is infinite.
To talk about an n-velocity, we need information of the function at $n$ points. For example, if we talk about acceleration (2nd derivative), we need the function's values at three points.
This could be, for instance understood by seeing the first principles definition of the derivative(*):
$$f''(x) = \lim \frac{f'(x+h) - f'(x)}{h} = \lim \frac{ \left(\frac{f(x+2h) - f(x+h)}{h} \right) - \left(\frac{f(x+h) -f(x)}{h} \right) }{h}$$
Now, the thing is the second derivative contribution can only be captured if we have a sampling of points $ \geq 2$
If we invert for the second $f(x+2h)$, we have (using $f(x+h)=f(x) + f'(x)h$:
$$ f(x+2h) = f(x) + 2hf'(x) + h^2f''(x)$$
Similarly, we can find
$$ f(x+3h) = f(x) + 3 hf'(x)+ 3h^2f''(x) + h^3f'''(x)$$
We'd find that in general, we have :
$$f(x+nh) = f(x) + \binom{n}{1} hf'(x) + \binom{n}{2} h^2 f''(x) +...$$
Now why does this feel a binomial expansion? That's answered in the section of "what is the meaning of all this?", if you can accept the result for now, then you can continue reading continously through the next sections.
Direct calculation of (*):
Write $$ \begin{align}f(x+h) &= f(x+ \frac{h}{2} + \frac{h}{2})\\ &= f(x+\frac{h}{2}) + f'(x+ \frac{h}{2}) \frac{h}{2} \\ &= f(x) + \frac{h}{2} f'(x) +\left[ f'(x) + f''(x) \frac{h}{2} \right] \frac{h}{2} \\ &= f(x) + f''(x)h + f''(x) \frac{h^2}{4} \end{align}$$
A three way split would allow you to calculate $f(x+h)$ with a three split=
Intuitive calculation of $(*)$ [how you should have actually done it]
You could think of $f(x)$ as measuring distance of an accelerating car travelling, $a$ be the first point in time and $b$ being the final point. We introduce a point in the middle $a+ \frac{b-a}{2}$ to involve the second derivative.
The contribution of velocity to the change over this whole interval would be $ f'(a) (b-a)$, what about acceleration? Well suppose we gain velocity $\delta v$ in $\frac{b-a}{2}$ seconds, then for that velocity can only effect the distance in the next $\frac{b-a}{2}$ seconds. Hence, we have:
$$ f(b) = f(a) + f'(a) (b-a) +( f''(a) \frac{b-a}{2} \frac{b-a}{2}) = f(a) + f'(a)(b-a) + f''(a) (\frac{b-a}{2})^2$$
Now, still you'd be confused since there is an additional fact of $1/2$. Obviously, this is not a good approximation since, if slice the time interval more finely then even the most finest slices acceleration would be contributing every other second, so we'd have to take the formula of $f(x+nh)$ formula with $n \to \infty, h \to 0, nh=b-a$
How would get the taylor from the approximation based on the n-point sampling?
If we want to approximate $f(a+b)$ provided $f(a)$, we do:
Setting $nh=t = b-a$, we have:
$$ f(x+t) = f(x) + \frac{ \binom{n}{1}}{n} tf'(x) + \binom{n}{2} t^2\frac{f''(x)}{n^2} ...$$
We find that as $n \to \infty$ the above expression turns to,
$$ f(x + t) = f(x) + tf'(x) + \frac{t^2}{2!}f''(x)..$$
and so on.
Now, what on earth is the meaning of all this?
This is probably the most interesting and conceptually rich section in this post, as these ideas is used even in the most advanced calculus calculations (eg: . So, buckle up!
We have the same premise as before, we want to approximate $f(x)$ at $a+b$ provided $f(x)$ at $a$, we split the interval $\left[a, b \right]$ into $\left[ a , a+h \right] , \left[ a+h , a+2h \right] \cdots \left[ a+(n-1)h , a+nh=b \right] $
So, we will calculate the taylor by approximating in steps. First question: How does the value of the function change from $\left[ a, a+h \right]$? we have by linear approximation:
$$ f(a+h) = f(a) + f'(a) h $$
But let's right this in a different way, we write as:
$$f(a+h) = \left[(1 + h \frac{d}{dx}) f(x)\right]_{x=a}$$
We can see this is the same as the previous result by unpacking everything (let me know if this step wasn't clear).
Now, how does the value of the function change on the interval $\left[ a+h , a+ 2h \right]$?
$$ f(a+2h) = f(a+h) + h f'(a+h)$$
What happens if we use the previously mentioned trick? We have:
$$ f(a+2h) = \left[ (1 + h\frac{d}{dx}) f(x+h)\right]_{x=a}$$
But, hey we can do the trick again on the inner $f(x+h)$, we have:
$$f(a+2h) = \bigg[ (1 + \frac{d}{dx}) \left[ (1+ \frac{d}{dx}) \right] f(x) \bigg]_{x=a}$$
Now, we do another trick, we think of $(1+h \frac{d}{dx})$ as a function in itself, which takes functions and gives out functions. This is known as an operator. And, then, we we consider $(1+ h\frac{d}{dx})^2$ to be this map applied consecutively. We have,
$$f(a+2h) = \left[ (1+ h\frac{d}{dx})^2 f(x)\right]_{x=a}$$
By induction, we can show that:
$$f(a+nh) = \left[ (1+h \frac{d}{dx})^n f(x) \right]_{x=a}$$
Now, suppose we fix $n \cdot h = b-a$( number of partition * size of partition of b-a), and send the number of partitions to infinity, we have:
$$ \begin{align}f(b)= \lim_{ n \to \infty} f(a+nh)
&= \lim_{n \to \infty} \left[ ( 1 + h \frac{d}{dx})^n f(x) \right]_{x=a} \\ &=\left[\lim_{n \to \infty} ( 1 + h \frac{d}{dx})^n f(x) \right]_{x=a} \end{align}$$
Now, here is something interesting, which we can show (try see why)
$$\lim_{n \to \infty} ( 1+ h \frac{d}{dx})^n = \lim_{n \to \infty} ( 1+ (\frac{b-a}{n} ) \frac{d}{dx})^n = 1+ (b-a) \frac{d}{dx} + \frac{(b-a)^2}{2!} {d^2}{dx^2} .. =e^{(b-a)\frac{d}{dx} }$$
We identify the operator series as evaluating the series for the exponential at the operator. Finally,
$$f(b) = \left[ e^{(b-a)\frac{d}{dx} } f(x) \right]_{x=a}$$
And that's it! That 's also the basis by the fancy shmancy category theory answer that tp1 wrote. It maybe remarked that the bracket evaluating trick thing I kept doing is also the basic idea for one shadowy version of calculus called Umbral Calculus
Why did this whole procedure "feel" like doing an integral?
See accepted answere here
Bonus : Shifting points of evaluation generally in higher calculus
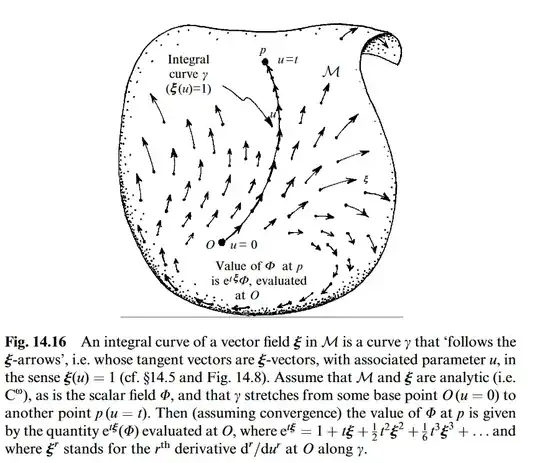
Roger Penrose road to reality
The idea of linear approximation is quite profound, and more general single variable calculus itself. If we are to think of abstractly, it says to find the value at a little bit away, we add at the inital point plus the change in parameter * the rate of change function with that parameter. We have,
$$E_h f(x) = ( I+ h \nabla_t) f$$
In another way, we can write the value of the function at a later point $x+h$ using the initial way with derivative. This idea works also in higher calculus to change the point of evaluation of a function on many different variables. To capture the idea of point of evaluation being changed, we we think of the curve as being made up a bunch of tiny tangent vectors , and by some math magic, associate the change in the output as we move along these tangent vectors as a derivative operator acting on the function. Once, we have that last line, then we can immediately use the taylor series idea to shift the evaluation point of the function.
