3

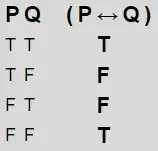
If we are given that propositions P and Q can never be true, is it still accurate to say that P and Q are necessary and sufficient for each other, and why?

I am conflicted here, as the statement P iff Q is true here and I have learned that this also means P and Q are necessary and sufficient for each other (for context, I have learnt that P is necessary for Q if P must be true to conclude Q is true, and that P is sufficient for Q if Q must be true to conclude that P is true); however, it seems counterintuitive to stipulate conditions for propositions being true (by deeming other propositions as necessary or sufficient for them) if these are never relevant to the situation, as these propositions are always false anyway.

I would appreciate an answer grounded in an explanation of necessity and sufficiency.

ryang
  • 38,879
  • 14
  • 81
  • 179
Princess Mia
  • 2,403
  • 1
    "it seems counterintuitive to stipulate conditions..." Are you comfortable with vacuously true statements? This is just more of the same as that. – JMoravitz May 24 '23 at 03:04
  • @JMoravitz thanks for the reply; so is it the case that notions of necessity and sufficiency apply to the statement P⇒Q when both these are false? Would you be able to explain how this is the case from the definitions of necessity and sufficiency? (I am not seeing them apply here) – Princess Mia May 24 '23 at 03:09
  • I think your difficulty hinges on your use of the word "relevance". In the everyday logic of mathematics, we don't care about relevance, we just care about mathematical facts: if $P$ and $Q$ are both false, they are equivalent. There are modal logics which attempt to model notions like relevance and necessity which we often use to qualify statements that we make in natural language. These logics are very interesting, but much harder to work with than the everyday logic of mathematics. – Rob Arthan May 24 '23 at 21:07

3 Answers3

7

Clearly, $$(¬P∧¬Q)\implies (\lnot P↔\lnot Q);$$ by contrapositive, $$(¬P↔¬Q)\implies(P↔Q).$$ So, by transitivity, $$(¬P∧¬Q)\implies(P↔Q);$$ that is, $$(¬P∧¬Q)→(P↔Q)$$ is a tautology. After all, P ↔ Q ($P$ and $Q$ necessary and sufficient for each other) just means that $P$ and $Q$ have the same truth value (in this case, 'false').

it seems counterintuitive to stipulate impossible—thus, irrelevant—propositions as conditions for propositions being true

But a contradiction $\bot$ within a conditional statement is not an irrelevant condition, since it is meaningful to truth evaluation:

  • $⊥$ is a sufficient condition for $P\quad\equiv\quad\top$
  • $⊥$ is a necessary condition for $P\quad\equiv\quad\lnot P;$

in order to truthfully assert that 'pigs can fly' is a necessary condition for $P,$ $P$ must be something false; on the other hand, whatever $P$ stands for, the assertion that 'pigs can fly' is a sufficient condition for $P$ is certainly a redundancy. Like vacuous truth, these assertions are perhaps surprising but not really counterintuitive, so I may be misunderstanding your point.

ryang
  • 38,879
  • 14
  • 81
  • 179
  • Can’t this be proven constructively to show it’s valid in more than just classical logic? Also, don’t you think necessary and sufficient conditions deal more with strict implication? We don’t want random a co-incidence between $A$ and $B$ to constitute that $A$ is necessary and sufficient for $B$. – PW_246 May 24 '23 at 12:29
  • 1
    @RW_123: yes, this can be proved constructively (and the proof is simpler): if you have $\lnot P$, $\lnot Q$ and $P$, you can infer $\bot$ and then infer $Q$ by ex falso quodlibet, so $(\lnot P \land \lnot Q) \to (P \to Q)$. Swapping $P$ and $Q$ you get $(\lnot P \land \lnot Q) \to (Q \to P)$, so $(\lnot P \lnot Q) \to (P \leftrightarrow Q)$ – Rob Arthan May 24 '23 at 20:53
4

In mathematics, "P is necessary for Q" is defined as meaning "it is impossible for P to be false and Q to be true." If both P and Q are totally impossible, then it's certainly impossible for P to be false and Q to be true, so we say that P is necessary for Q.

Likewise, in mathematics, "P is sufficient for Q" is defined as meaning "it is impossible for P to be true and Q to be false." If both P and Q are totally impossible, then it's certainly impossible for P to be true and Q to be false, so we say that P is sufficient for Q.

These conclusions may be at odds with the everyday meanings of the words "necessary" and "sufficient." However, when we're writing about math, we use the mathematical definitions of these words, not the everyday meanings.

Tanner Swett
  • 10,624
  • This is the answer I was composing in my head while staring at the page. Very well stated. To reiterate: the everyday meanings of necessary and sufficient break down when you start to talk about impossible situations. – Matthew Leingang May 24 '23 at 13:16
  • How are the everyday and mathematical meanings of 'necessary' and 'sufficient' actually discrepant? – ryang May 24 '23 at 18:13
  • @ryang Well, I think that most people would agree that walking to the moon and walking to Mars are both totally impossible, yet most people would disagree with the sentences "in order to walk to Mars, it is sufficient to walk to the moon" and "in order to walk to the moon, it is necessary to walk to Mars." On the other hand, if P = "I am going to walk to the moon" and Q = "I am going to walk to Mars," by the mathematical meanings, P and Q are necessary and sufficient conditions for each other. These two ways of looking at things seem to be at odds with each other. – Tanner Swett May 24 '23 at 21:09
  • All that being said, it's not clear that there really is a discrepancy between the two notions, which is why I wrote "may be at odds" instead of "are at odds." – Tanner Swett May 24 '23 at 21:10
  • @TannerSwett Thanks for elaborating! I am reminded of this discrepancy: in mathematics, 'only if' means implies, whereas in everyday English that phrase strongly (and not unreasonably) suggests 'just if', i.e., if and only if. – ryang May 25 '23 at 05:17
1

If $P$ and $Q$ can never be true, are they still "necessary" and "sufficient" for each other?

The "can never be true" is distracting. In propositional logic, we don't make predictions about the future. We talk about what is true (present tense). Change it to:

If $P$ and $Q$ are both false, are they "necessary" and "sufficient" for each other?

Then the answer would be, yes.

Truth Table for $P\iff Q$

enter image description here

See line 4 where $P$ and $Q$ are both false.

Dan Christensen
  • 14,529