This is a fascinating problem! I was able to come up with a partial proof, proving some results and bounds. Specifically, when $n = 3$, the maximum is exactly $3$. For $n>3$, the maximum is at least $4$ (proven constructively). For all $n$, the number of intersections is no more than $n$. And because of that, when $n = 4$, the maximum is exactly $4$. In sum:
- $n=3$: max is $m=3$
- $n=4$: max is $m=4$
- $n \geq 5$: max is $4 \leq m \leq n$
Upper bound (medium): There are at most $n$ intersections.
For any "outer" polygon $A$ (regular with sides $n$) and inner polygon $B$ (regular with sides $n+1$), consider the bounding circle of $B$. This circle passes through $A$ at most $2n$ times (twice on each edge), and these are the only places where $B$ might intersect $A$. Since $B$ cannot select both intersections on the same edge of $A$ (else that would create a collinear edge), there are at most $n$ intersections.
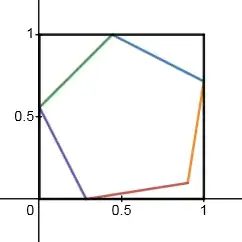
Note that this contradicts your conjecture when $n < 4$. Specifically, when $n = 3$, we can only have $3$ intersections. Actually, we can achieve this upper bound:

The point at the bottom is a midpoint, which allows the other two vertices to touch exactly (there are other ways to do it, but that's easiest to prove).
Corollary (near-trivial): For $n = 3$, the maximum number of intersections is $3$.
The diagram above constructively shows a solution with three vertices, and per the upper bound it cannot be higher than this. It follows that the true maximum is $3$.
Lower bound (easy): There are at least $2$ intersections.
We will get a stronger bound later, but it's much easier to lower-bound it with $2$ by doing something like the following prototypical construction:

Basically just make $B$ smaller than a side of $A$ and shove it in a corner where it touches two sides in two places. The one vertex of $A$ turns by $2\pi/n$ and the two vertices of $B$ together turn by $4\pi/(n+1)$, which is always (i.e. for $n>1$) more, so $B$ never intersects those edges in more than two points, and it can't intersect any other edges because it's smaller than a side of $A$.
Lemma (easy): All intersections lie on the interior of edges.
Suppose by way of contradiction that an intersection $p$ could lie on a vertex of $A$. Because the turning angle of $B$ is smaller than that of $A$, at least one of the connected edges in $B$ would fall outside of $A$. Thus, $p$ must lie on the interior of some edge $e_1$ of $A$.
Lemma (easy): Given a neighbor of an intersection, it can only intersect $A$'s next edge.
From the previous lemma, we know that a given intersection $p$ lies on the interior of $A$'s edge $e_1$. Consider neighbor $q$ of $p$ in $B$.
If $q$ intersects $A$, then it cannot be on the same edge $e_1$, because $p$ is already on it, and this would create a collinear edge. Also note that the side lengths of $B$ must be strictly shorter than those of $A$ (else $B$ cannot fit inside $A$). Hence, by the triangle inequality, $q$ cannot lie on anything but neighbor $e_2$ of $e_1$, if it lies on $A$ at all.
Lower bound (harder): For $n \geq 4$, there are at least $4$ intersections.
Here is a constructive proof that for $n \geq 4$, there are at least four points.
Consider the following prototypical diagram:
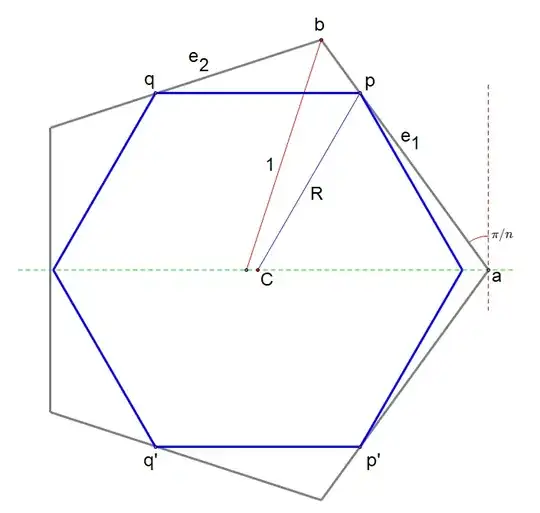
We have the outer polygon in gray and the inner polygon in blue. The polygons are both aligned so that their rightmost vertex is on the $x$-axis. WLOG $A$ has radius $1$, so $a = \langle 1, 0 \rangle$. We can also see that $b = \langle \cos(2\pi/n), \sin(2\pi/n) \rangle$. The inner polygon $B$ has center $C = \langle x_C, 0 \rangle$ and radius $R<1-x_C$ (note that this means that its rightmost vertex does not intersect $A$).
The angle (marked) at $a$ from the vertical to the polygon is $\pi/n$ (that plus the same angle on the other side have to add up to $2\pi/n$, the amount turned at each vertex). Thus, the slope of polygon $A$'s edge $e_1$ is $-\cot(\pi/n)$. With point $a$ and the slope, we can use the point-slope form of a line to get:
$$
(y-0) = (-\cot\theta) (x-1)\text{,}\hspace{1cm}\text{where }\theta:=\frac{\pi}{n}
$$
We would like $p$ to lie on this line and further, it must be a vertex of $B$ as per:
\begin{alignat*}{2}
x &= x_C ~+~ && R \cos(2\phi)\text{,}\hspace{1cm}\text{where }\phi:=\frac{\pi}{n+1}\\
y &= && R \sin(2\phi)
\end{alignat*}
Substituting the latter into the former, we get a linear equation in $R$ and $x_C$:
$$
R \sin(2\phi) = -\cot\theta( x_C + R \cos(2\phi) - 1 )
$$
We now proceed similarly. The slope of $e_2$ can now be found as a rotation of the vector defining $e_1$. Its slope works out to be $-\cot(3\theta)$ (remember your trig identities, kids). Combined with the point $b$ and this slope, we can define the line $e_2$ from point-slope form. We know that $q$ is on the inner polygon $B$, and we can intersect these to get a second linear equation in $R$ and $x_C$.
$$
R \sin(4\phi) = -\cot(3\theta)( x_C + R \cos(4\phi) ) + \cot(3\theta)\cos(2\theta) + \sin(2\theta)
$$
We now have two linear equations in $R$ and $x_C$, so we can combine them and solve for their intersection (i.e., the values of $R$ and $x_C$). This appears to be unavoidably messy, but ultimately it's closed-form and always possible.
Here are some values up through $n = 10$ to demonstrate, rounded to 6 sigfigs:
| n |
$x_C$ |
$R$ |
| 3 |
0.0490381 |
0.549038 |
| 4 |
0.0514622 |
0.752764 |
| 5 |
0.0486795 |
0.842470 |
| 6 |
0.0451871 |
0.888297 |
| 7 |
0.0418499 |
0.914587 |
| 8 |
0.0388455 |
0.931084 |
| 9 |
0.0361838 |
0.942190 |
| 10 |
0.0338318 |
0.950094 |
def calc_params(n):
theta = pi / n
phi = pi / (n+1)
#Two linear equations, of form A R = B x_C + C
A1 = sin(2*phi) + cos(2*phi)*cot(theta)
B1 = -cot(theta)
C1 = cot(theta)
A2 = sin(4*phi) + cos(4*phi)*cot(3*theta)
B2 = -cot(3*theta)
C2 = cos(2*theta)*cot(3*theta) + sin(2*theta)
#Solve (divide through by first coeff and sub)
B1/=A1; C1/=A1
B2/=A2; C2/=A2
x_C = (C2-C1)/(B1-B2)
R = B1*x_C + C1
return x_C, R
Here's $n=3$ through $n=8$, just for an intuition:

Thus we have two points $p$ and $q$ that are intersections of $A$. Because of the symmetry over the $x$-axis, since $p$ and $q$ are intersections, $p'$ and $q'$ are also. Together, that is four intersections. Because we can solve these equations always, we have at least $4$ intersections (except in the case $n = 3$, where $q = q'$, so there are only three unique intersections).
Corollary (near-trivial): For $n = 4$, the maximum number of intersections is $4$.
Per the former lower bound and the above upper bound, we have exactly $4$ instersections for $n=4$.