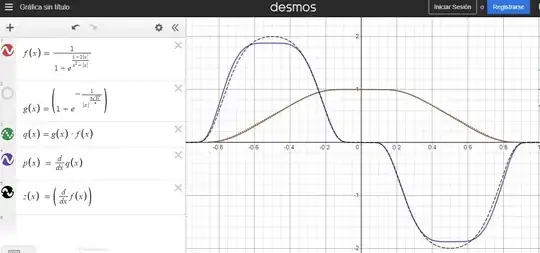
Are these smooth bump functions $\in C_{0}^{\infty}(-1,\ 1)$? $f(x) = \left(1+\exp\left(\frac{1-2|x|}{x^2-|x|}\right)\right)^{-1}$ and related
Trying to find an answer to this other question, I took a function from this answer to other question and modified it to make:
- $$f(x) = \frac{1}{1+e^{\frac{1-2\ |x|}{x^2-|x|}}},\quad x\in(-1,\ 1)$$ which look like a smooth bump function, but since it contain absolute value functions within, so I don't know if at some derivative it will fail to be class $C^\infty$.
Also, by taking the derivative of $f(x)$ I found that it looses its flat top so it cannot be solving some Delay differential equation as the asked in the mentioned question: $f'(x)=2\ f(2x+1)-2\ f(2x-1),\,f(0)=1,\,x\in(-1,\ 1)$ which required the "new lobes" to keep the form of the original function. So by playing with functions I found this in Desmos:
- $$q(x) = \frac{1+e^{\frac{-1}{|x|^{\frac{3}{4}\sqrt{2\pi}}}}}{1+e^{\frac{1-2\ |x|}{x^2-|x|}}},\quad x\in(-1,\ 1)$$ which I know beforehand don't solve the presented delayed differential equation since its derivative maximum is not $2$, but at least it keep at some extent the flat top shape.
So I would like to know if these functions $f(x)$ and $q(x)$ are smooth bump functions.
Bonus track: There is a "simple" Delay Differential Equation (DDE) solved by $q(x)$?, I am trying to find something similar to the scaled/displaced version of the Fabius function that solves the DDE: $\varphi'(x)=2\varphi(2x+1)-2\varphi(2x-1)$ when $|x|\leq 1$.
PS: in this answer you could see a comparison of a numerical implementation of the Fabius function $\text{FabiusF}(x+1)$ against $q(x)$ and fit relatively good for $|x|<1$.