Solving $x''+x+\text{sgn}(x')\sqrt{|x'|} = 0\ $ Does it have closed form solutions? Does it stop moving? Could it stop at a different place than zero?

Question

Solving $x''+x+\text{sgn}(x')\sqrt{|x'|} = 0\ $

• Does it have closed form solutions? Please show how you got them.
• Does it stop moving? There exists a finite extinction time $|T|<\infty$ such $x'(t) = 0,\ \forall t\geq T$. Which is the formula of $T$ given the initial conditions?
• Could it stop at a different place than zero? It is possible for its solutions to stop moving at a constant value $x(T) \neq 0$ such as $x(t) = x(T),\,\forall t>T$ (this was answered in the comments by @aghostinthefigures - turns out it can only stop moving at $x(T) = 0$).

---

Added later

In the following paper A note on the dynamics of an oscillator in the presence of strong friction, in the Proposition 2.3 tells that these kind of ODEs could have solutions of finite duration, and in Theorem 3.1 tells that are least there are 2 orbits that do the trick, but unfortunately is "too advanced" for me: I am not completely sure if the same equation is considered (I think is the case $\alpha = \frac12$), neither if is possible to find the finite extinction time $T$ from the formulas explained there and initial conditions. Maybe someone more experienced in Diff. Eqns. Analysis could use it to solve part 2.

---

Motivation_____________ (not required for giving an answer)

After learning from this paper that the only possible way from a ODE for standing solutions that stop moving, it is if the differential equation have at least one Non-Lipschitz point in time. I have got really interested in them since everything I learned in engineering were modeled through solutions that can be represented through Power Series, which cannot represent this behavior (since matching a constant value forever will violate the Identity Theorem).

I have made a lot of question trying to understand differential equations that stop moving in this tag [finite-duration] since I have not find a specific theory with their treatment contained it in just one place, by instead spread in many other topics without a deep insight.

Since every "small-angle approximation" and/or "linearization" will destroy the Non-Lipschitz component (as example, when using Perturbation theory), its solutions cannot represent accurately the moment when system stop moving.

I review in the question A brick sliding in an horizontal plane after an initial push... the simplest physics example which show, as example, a polynomial decay instead of the exponential decay expected for a solution of a Linear ODE. The answer is quite simple from energy analysis, which is good since show the closed-form solution founded is working ok.

But most interestingly, the next step in complexity was introducing friction (Coulomb's Friction), and the answer become totally not obvious: I reviewed it in the question Closed-form solutions to $x''+\frac{k}{m}\ x+\mu\ g\ \text{sgn}(x')=0$ and the solutions show three things:

• There exist closed-form solutions as it where found by @eyeballfrog in his answer
• The solutions' speed profile indeed achieve a finite extinction time where its becomes zero after a finite time $0<T<\infty$.
• The solution could stop moving in a position different from equilibrium, such as $x(T) \neq 0$, which so far I know it is impossible to be achieved by any classic differential equation thought in undergraduate engineering physics classes (surely is impossible is the ODE is linear or if it solved through a power series: if you know some other kind of counter-examples, please share them here).

Since traditionally a physics' model required the ODE to be Autonomous, there is no many "simple possible" ways to make the ODE Non-Lipschitz, been already studied in the mentioned question the scenario $\text{sgn}(v)$, here I ask for the next possible alternative $\text{sgn}(v)\sqrt{|v|}$ discussed in the mentioned paper and that could have some applications like in this other question. (Update: due the answer in the comments by @aghostinthefigures proving that only something of the form of $\text{sgn}(v)$ could stop moving in a place different from zero, I believe its a more accurate model now).

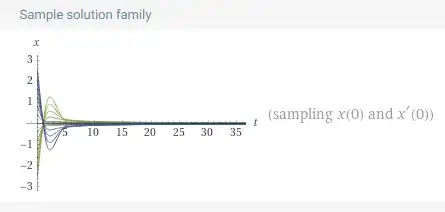
So far from Wolfram-Alpha, it can be seen their solution could resemble an exponential decay "at the end" (where oscillations disappears), but is not clear if they are really achieving a finite extinction time when its stop moving, neither if is possible to stop moving in a position different from zero.

I would like to understand if this example could be exploitable as an alternative for the traditional simple harmonic oscillator for modelling the physics of phenomena that stop moving (at least near the stopping time, like a non-linear version of the "small angle approximation" for these systems), as maybe could be used also the example reviewed in the mentioned question $x''+x+\text{sgn}(x')=0$ (preferred one in my opinion after @aghostinthefigures comment).

I Hope you found it as interesting as I do.

Answer 1

$$\frac{d^2 x}{dt^2}+x(t)+\text{sgn}\left(\frac{dx}{dt}\right)\sqrt{\Bigg|\frac{dx}{dt} \Bigg|}=0$$ This second order ODE of autonomous kind can be reduced to a first order ODE thanks to the change of function : $$\frac{dx}{dt}=y(x(t))\quad\implies\quad \frac{d^2 x}{dt^2}=\frac{dy}{dx}\frac{dx }{dt}=y\frac{dy}{dx}$$ $$\boxed{y\frac{dy}{dx}+x+\text{sgn}\left(y\right)\sqrt{\big|y \big|}=0}$$ Consider the range where $y>0$ and let $y=z^{-2}$ . The ODE becomes : $$y\frac{dy}{dx}+x+\sqrt{y}=0$$ $$\frac{dz}{dx}=\frac12 z^4+\frac12 xz^5$$ This is an Abel's differential equation of first kind and fith degree : https://mathworld.wolfram.com/AbelsDifferentialEquation.html

In the general case this kind of equation cannot be solved in terms of a finite number of standard functions (elementary and special standard functions). Similarly on the range $y<0$.

This answers as NO to the question "Does the PDE has closed form solutions ? ". Of course this isn't an answer to the others more interesting questions.

Answer 2

Is there a closed form solution? Likely not.

Write it as follows:

$$x''+x+\frac{x'}{\sqrt{|x'|}}=0.$$ Now, assuming one has found a solution $w$, or a convenient $w$, the other solution is obtained as follows: let $x=wy$ so that

$$((wy)’’+wy)^2=|(wy)’|,$$ which, assuming $x>C$ for some constant $C$, or that $$(x’’+x)^2=q_0x’$$ needs to be solved for general constant $q_0$, letting it be 1 or -1 depending on the sign of the derivative, we get, choosing $w’’+w=0$, $$((wy)’’+wy)^2=q_0(wy)’\\ (2w’y’)^2=q_0(w’y+y’w)\\ 4w’^2y’^2-q_0wy’=q_0w’y.$$ Now if $y,y’$ were swapped, we’d be in the domain of the familiar. However, we now wish to solve the form $$Py’^2+Qy’+Ry=0.$$ Using $y=\int \eta, $ we can obtain the form equivalent to $$A\eta^2+B\eta\eta’+C\eta+D\eta’=0$$and after letting $\eta=\lambda u$ and $A\lambda +B\lambda’=0$ we get $$B\lambda^2uu’+(C\lambda+D\lambda’)u+D\lambda u’=0$$ or $$Luu’+Mu+Nu’=0.$$ Now, $$A=(P/R)’=4q_0w\\ B =2P/R=-8q_0w’\\ C=1+(Q/R)’=1+(w/w’)’\\ D=Q/R=w/w’.$$ And, $$\lambda =C_0e^{\int \frac{w}{2w’}}$$ thus $$\therefore x=w\left(C_1+C_0\int e^{\int \frac{w}{2w’}}u\right).$$

---

For $u,$ $$u’=-\frac{Mu}{Lu+N},$$ which is an interesting case of the general form, $$\boxed{\boxed{u’=\frac{\alpha u+\beta}{\gamma u +\delta}}}.$$ Solving explicitly for $u$ requires new theory.