Suppose $x$ and $y$ are two positive numbers satisfying the equation $x^y = y^x .$ Which of the following are true?
(a) For all $x > 1,$ there always exist a $y > x$ such that the above equation holds.
(b) For all $x > e$ there is always a $y > x$ such that the above equation holds.
(c) For all $1 < x < e$ there is always a $y > x$ such that the above equation holds.
(d) If $x < 1,$ the y must be equal to $x.$
I was struggling with this problem for a long time. I was primarily focussing upon the idea, that $x^y = y^x$ has solutions $(x,y)=((1+\frac 1t)^t,(1+\frac 1t)^{t+1}),$ where $t\in\Bbb R^*.$ Using this,I tried hovering over the options given.
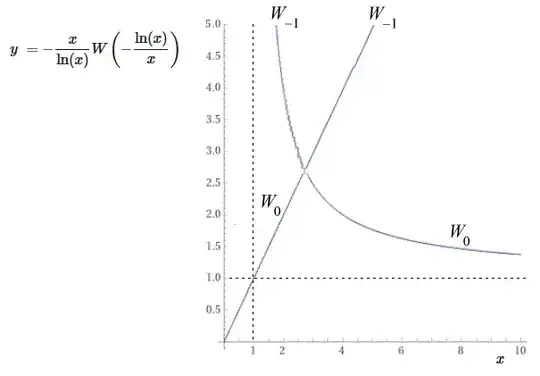
EDIT: As mentioned by @Macavity, this approach stands invalid, as the parametric solution, I considered here, is not covering all the solutions of the given equation (if I understand him correctly). I proceeded following his suggestions by considering the graph of $\frac {\ln x}{x}$. To have a look at it please proceed further and my new attemt is marked with an italics case to make it easier to comprehend.
We first consider the case,when $x=y$, then, $(1+\frac 1t)^t=(1+\frac 1t)^{t+1}$. Assuming, if $(1+\frac 1t)\neq 0$, then, $$1=(1+\frac 1t)\implies \frac 1t=0,$$which is absurd. If, $$(1+\frac 1t)=0,$$ then, $t=-1.$ We observe, $x=y$, only if, $t=-1$, which implies $x=0,y=0.$ So, we can safely conclude the option D is incorrect.
Now, we try to determine, the case, when $x>y$ i.e this is possible only when $$(1+\frac 1t)^t>(1+\frac 1t)^{t+1}\implies 1>(1+\frac 1t)$$, this is true, under the assumption, $(1+\frac 1t)^t>0.$ Now, $$(1+\frac 1t)<1\implies \frac 1t<0\implies t<0.$$ So, we conclude, $x>y$ if $t<0.$ Similarly, we say, $x<y$ only if, $t>0.$ But, if $t>0$, then, $x,y>0.$ So, we can say, option $A,B$ and $C$ are observe to hold good with this derived result. Hence, the answer is options $A,B$ and $C.$
However, the answer is given as option $C$ and $D.$ I don't quite find any error in my approach. I am confused about this. I am unsure, whether I missed something basic or not.
My second attemt, following @Macavity's suggestion, goes like this:
I tried sketching the graph of $y=\frac{\ln x}{x}$. It matched with this,
Then, I proceeded with a simplication of the question. Any solution, of the equation, $\frac{\ln x}{x} =\frac{\ln y}{y}$ is also a solution of the equation, $x^y = y^x.$ But the converse might not be true. Then, I again started hovering over the given options, and I started with option $A$:
Option $A$ states, that, " For all $x > 1,$ there always exist a $y > x$ such that the above equation holds." Now, if this condition satisfies, then it means, for each $x>1$ we will find a $y$ such that the ordered pair $(x,y)$ is a solution of the given equation, and also of the equation, $\frac{\ln x}{x} =\frac{\ln y}{y}$, as $x>1.$ Now, from the graph of the function $y=\frac{\ln x}{x}$ it can be easily verified, that this is not the case since, the function $\frac{\ln x}{x}$ is strictly increasing when $1<x<e$ and strictly decreasing when $x\geq e$. So, $Option A$ is incorrect.
Next, we try to verify the validity of option $B$:
In option $B$ it is presented, that "For all $x > e$ there is always a $y > x$ such that the above equation holds." Now, similar to the above reasonining we may conclude, $B$ is incorrect. This is because, if this condition satisfies, then it means, for each $x>e$ we will find a $y$ such that the ordered pair $(x,y)$ is a solution of the given equation, and also of the equation, $\frac{\ln x}{x} =\frac{\ln y}{y}$, as $x>e.$ Now, from the graph of the function $y=\frac{\ln x}{x}$ it can be easily verified, that this is not the case since, the function $\frac{\ln x}{x}$ is strictly decreasing when $x>e.$ So, $Option B$ is incorrect.
Now, we proceed to check the validity of Option $C$ :
In option $C$ it's asserted that " For all $1 < x < e$ there is always a $y > x$ such that the above equation holds." We proceed like the previous two cases. If this condition satisfies, then it means, for each $1<x<e$ we will find a $y$ such that the ordered pair $(x,y)$ is a solution of the given equation, and also of the equation, $\frac{\ln x}{x} =\frac{\ln y}{y}$, as $x>1.$ Now, from the graph of the function $y=\frac{\ln x}{x}$ it can be easily verified, that this is the case since, the function $\frac{\ln x}{x}$ is strictly decreases when $x>e,$ and as seen on the graph, the $y$ co-ordinate again takes all the values that were taken previously when $x$ was in the range $1<x<e.$ So, $Option C$ is correct.
Now, we proceed to validate, $Option D$ :
In Option $D$ it is asserted that "If $x < 1,$ the y must be equal to $x.$" We proceed like the other cases. If this condition satisfies, then it means, for each $x<1$ we will find a $y=x,$ such that the ordered pair $(x,y)\equiv (x,x)$ is a solution of the given equation, and also of the equation, $\frac{\ln x}{x} =\frac{\ln x}{x}$, if $0<x<1.$ Now, from the graph of the function $y=\frac{\ln x}{x}$ it can be easily verified, that this is the case,if $0<x<1$ since, the function $\frac{\ln x}{x}$ is strictly increasing when $0<x<1.$ So, $Option C$ might be correct. We can't argue about about the case, when $x<0$ as $y$ is not defined there. So, we can't be sure of Option $D$. Nevertheless, this is the only option left and the question states Only two options are correct. Hence, $Option D$ should be the correct option.
I feel the issue is now resolved, my answers are now matching with the given one. I think my approach, now is devoid of any more loopholes. Thanks to @Macavity, for the useful suggestions. Indeed, graphs are nice little ways, to solve these sorts of problems.
I saw, or realize (rather,) that some users don't advocate the usage of images in this site. But I couldn't help it, as without the help of the image of the graph, I couldn't quite explain myself or my reasonings sufficiently and optimally.