Are there any concentration bounds of the following form: $$ \Pr_{x \in \mathbb{S}^{n-1}(R)}[|x_1+\cdots+x_n|\geq 1] \leq \text{function}(n,R) $$ The radius $R$ should be considered as a constant and the dimension $n$ should be thought of as growing to infinity. I tried to calculate the $n$-dimensional integral, but it doesn't look wieldy.
1 Answers
Yuval Filmus observed that, since the uniform distribution on the sphere is rotation-invariant, the required probability should be the same as the probability that a single coordinate is more than $1/\sqrt{n}$ in absolute value.
Hence, $$ \Pr_{x \in \mathbb{S}^{n-1}(R)}[|x_1+\cdots+x_n|\geq 1] = I_{\frac{R^2-\frac{1}{n}}{R^2}}(\frac{n-1}{2},\frac{1}{2}) $$
where $I$ is the Regularized Beta Function. See this answer for an explanation and reference.
In the discussion below, I take $R=2$. Some observations from Mathematica:
Plot 1:
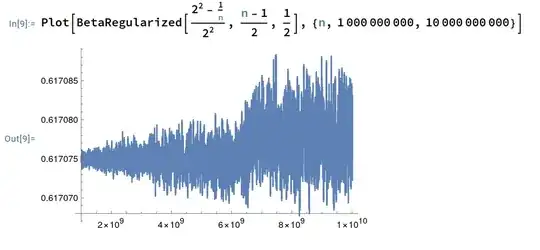
Plot 2:
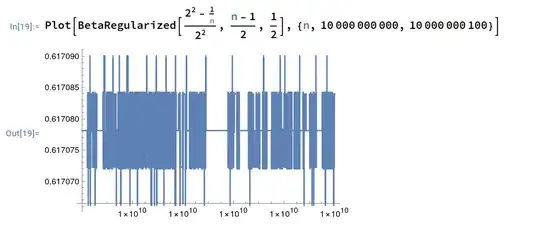
I tried to find the liminf of this function, but Mathematica couldn't calculate it:
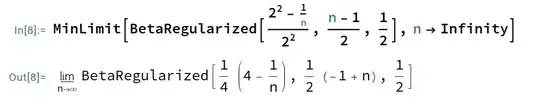
Table of values of this function at some very large values of n:

The function might have a limit as $n$ goes to infinity. The fluctuations in the graph might just be numerical inaccuracies. At any rate, it should be true that for $n$ large enough,
$$ 0.61 \leq \Pr_{x \in \mathbb{S}^{n-1}(2)}[|x_1+\cdots+x_n|\geq 1] \leq 0.62 $$
(The lower and upper bounds might be different for different values of $R \geq 1$, but should be constants, for $n$ large enough)
- 543
-
1Note that in the limit this is $2\Phi(-1/R)=2\Phi(-0.5)= 0.61707507745 $ where $\Phi$ is the standard normal cdf. You can get this by approximating some of the integrands with exponentials near the endpoints that matter as n gets large. – Eric Apr 29 '23 at 18:14