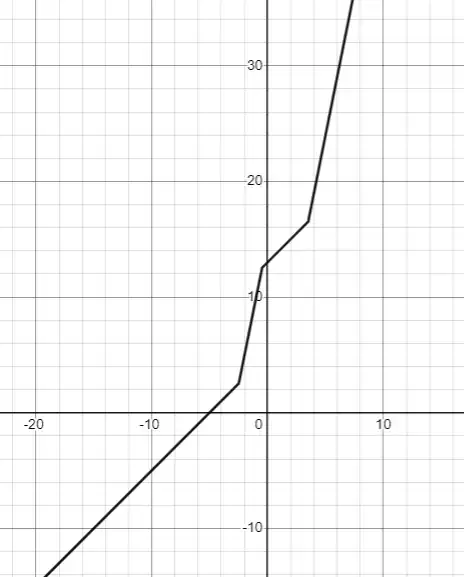
The idea of the problem exists in this website and this post may be a duplicate. I saw it a long time ago, but could not find it recently.
Say we have the following $n$ straight lines:
$$y=m_1x+c_1 \text{ when }-\infty<x<x_1$$
$$y=m_2x+c_2 \text{ when }x_1<x<x_2$$
$$y=m_3x+c_3 \text{ when }x_2<x<x_3$$
$$\vdots$$
$$\text{and so on}$$
$$\vdots$$
$$y=m_{n-1}x+c_{n-1} \text{ when }x_{n-2}<x<x_{n-1}$$
$$y=m_nx+c_n \text{ when }x_{n-1}<x<x_n$$
with $-\infty<x_1<x_2<x_3<\dots<x_n<\infty$.
The problem is to express these in one and only one equation. I do not remember how it looks exactly, but I am sure it involves the absolute value, something like:
$3x+2+|2x+7|+|7x-5|$, which merge $4$ straight lines. (Again, I am not sure about this exact form).
Using the values of $m$'s, $c$'s, and $x_j$'s, how to find that single equation, using only absolute values and coefficients of $x$'s and constant terms, and no more complications?
Your help would be appreciated. THANKS!