0

Let $\gamma : [a,b] \to \mathbb{R}^2$ be a continuous map which is injective on $[a,b)$ ( For example, simple closed curve ). Let $a_i \in [a,b]$ and $\delta>0$ be a small positive number. Then note that the image under $\gamma$ of $[a,b]-(a_i -\delta , a_i+\delta)$ is a compact set that does not contain $\gamma(a_i)$.

Then, can we choose $r$ small enough that $\gamma$ does not enter $\bar{B_r}(\gamma(a_i))$ except when $t\in (a_i -\delta , a_i+\delta)$ ?

In fact, this argument appears in the eleventh paragraph of the John Lee's Introduction to Riemannian manifolds, proof of the theorem 9.1 ( Rotation index theorem ).

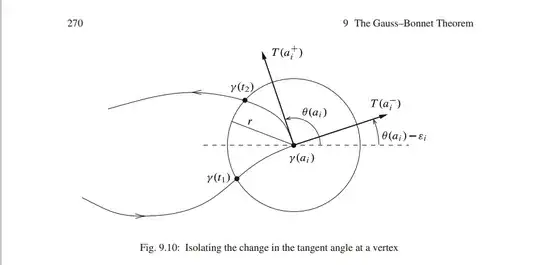
C.f. For a supplement, let's look at the next image :

enter image description here

Such a ball of radius $r$ exists?

Can anyone helps?

Plantation
  • 2,417
  • 1
    Why you say that the image does not contain $\gamma(a_i)$? Or equivalently why $\gamma(b)\neq\gamma(a_i)$? With this property the answer is "yes, we can choose such $r$". But otherwise of course "no". – freakish Apr 28 '23 at 11:34

1 Answers1

1

One way to answer this is to think of $\gamma(a_i)$ and $\gamma(([a,b]-(a_i-\delta, a_i+\delta))$ as disjoint compact subsets of $\mathbb{R}^2$. Hence there must be a minimum distance between them. And it can't be zero as that would imply the existence of a sequence of points in $\gamma(([a,b]-(a_i-\delta, a_i+\delta))$ converging to $\gamma(a_i)$. But that can't happen since $\gamma(([a,b]-(a_i-\delta, a_i+\delta))$ is closed, hence includes its limit points, hence must include $\gamma(a_i)$ which contradicts that they're disjoint.

Ben Ciotti
  • 246
  • Thanks. Can I ask further? Q. 1) Where the compactness of the $\gamma(a_i)$ is used in your argument? Anyway, I found an assoicated question : https://math.stackexchange.com/questions/391396/for-two-disjoint-compact-subsets-a-and-b-of-a-metric-space-x-d-show-that Q. 2) Why such a nonzero minimum distance implies the existence of such a closed ball of radius $r$? – Plantation Apr 28 '23 at 12:25
  • Perhaps, can you give me a hint??~ – Plantation Apr 29 '23 at 04:30
  • 1
    Compactness is equivalent to closed and bounded in $\mathbb{R}^n$. That's a famous theorem. So that's how I know they are closed. And then once you find a minimum non-zero distance just take a ball of radius less than that distance centered at $\gamma(a_i)$. – Ben Ciotti Apr 29 '23 at 18:28
  • 1
    Thank you very much. Certainly, if we let $0 < r < \inf{d(\gamma(a_i),b) : b \in B:=\gamma([a, a_i-\delta]\cup [a_i+\delta,b])} > 0 $, then for all $ t\in [a, a_i-\delta]\cup [a_i+\delta,b]$, $\gamma(t) \notin \bar{B_r}(\gamma(a_i))$. – Plantation Apr 30 '23 at 04:56
  • And can I ask a further interlude question? In proof of the Theorem 9.1 of the Lee's Riemannian manifolds, eleventh paragraph, he continues to argue as follows :"Let $t_1 \in (a_i-\delta ,a_i)$ denote a time when $\gamma$ enters $\bar{B_r}(\gamma(a_i))$, and $t_2 \in (a_i , a_i +\delta)$ a time when it leaves (C.f. Fig. 9.10 in my question)." Why such $t_1$, $t_2$ exists? – Plantation Apr 30 '23 at 04:56
  • 1
    $\gamma^{-1}(\bar{B}_r)$ is a closed subset of $(a_i-\delta, a_i+\delta)$, hence it has an infimum (as do all sets which are bounded below). This is your $t_1$. It is necessarily in the set by closure. – Ben Ciotti May 01 '23 at 21:57
  • For the final sentence in your comment, you mean $t_1 \in (a_i - \delta , a_i)$? Anyway, I somewhat understand. Thanks. – Plantation May 02 '23 at 02:40
  • 1
    More to the point, $t_1 \in \gamma^{-1}(\bar{B}_r) \subset (a_i-\delta, a_i+\delta)$. Actually though it might be a better idea to define $t_1$ as the supremum over $t<a_i$ of $\gamma^{-1}(\partial B_r)$. That way it is the last time the path enters $B_r$. Alternately you could define $(t_1, t_2)$ as the largest interval containing $a_i$ whose image under $\gamma$ is in $B_r$. – Ben Ciotti May 02 '23 at 04:05
  • O.K. What is the more formal definition of the supremum over $t<a_i$ of $\gamma^{-1}(\partial B_r)$? $ \sup ((a_i -\delta , a_i) \cap \gamma^{-1}(\partial B_r))$? It is somewhat ambiguous. And are you sure you chose supremum, not infimum? I want to make this issue more clear :) – Plantation May 02 '23 at 04:49
  • 1
    Supremum is the same as least upper bound. You can define $t_1$ both using a sup or an inf. $t_i=\inf {t \in (a_i-\delta, a_i) : \gamma (t_1, a_i)\subset B_r}$ will suffice. – Ben Ciotti May 02 '23 at 05:13
  • 1
    Uhm O.K. ! :) Thanks~ – Plantation May 02 '23 at 06:40