A few years ago, I saw an article that showed that it was possible to derive the power series for sine and cosine using a tail-to-tip chord approximation in the unit circle.
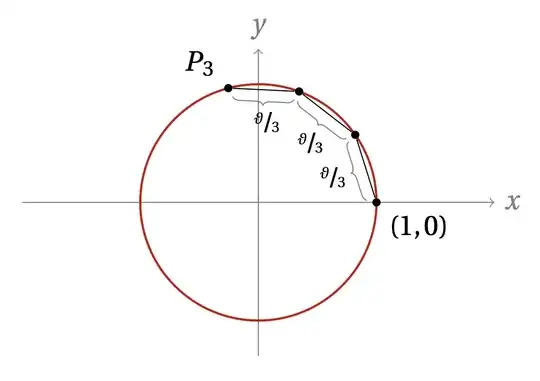
Basically, one first create a chord of length $0 \leqslant \theta \leqslant 2$ starting from the origin point $(1,0)$ to a point $P_1$ on the unit circle.
Now, if you divide the length $\theta$ by a given constant $n$ and create a sequence of multiple tail-to-tip chords, then you have $n$ points on the unit circle from $P_1$ to $P_n$ and the total length [of all chords] remains $\theta$.
You want to find the couple $(x_n,y_n)$ by solving the tail-to-tip recurrence system given by
$$ \begin{cases} (x_k - x_{k-1})^2 + (y_k - y_{k-1})^2 = \left(\frac\theta n\right)^2 \\ (x_k)^2 + (x_k)^2 = 1 \end{cases} $$
Trying to first the first couple $(x_1,y_1)$ we have
$$ \begin{cases} (x_1 - x_0)^2 + (y_1 - y_0)^2 = \left(\frac\theta n\right)^2 \\ (x_1)^2 + (y_1)^2 = 1 \end{cases} $$
And it's not hard to show that
$$ x_0 \neq 0, y_0 = 0 \implies x_1 = \frac{(x_0)^2 - (\theta/n)^2 + 1}{2x_0}, y_1 = \sqrt{1 - (x_1)^2} $$
We know that $P_0 = (1,0)$ so we can easily compute $P_1$ from the formula above. Further terms can be computed using iterative substitution, aka the "plug and chug" method. Indeed, we can show that
$$ x_0 \neq 0, y_0 = 0 \implies x_k = \frac{(x_{k-1})^2 - (\theta/n)^2 + 1}{2x_{k-1}}, y_k = \sqrt{1 - (x_k)^2} $$
Now, expanding this whole expression becomes very cumbersome for $k > 2$ and we want to find an explicit formula instead, that is, one which doesn't involve $x_{k-1}$ in the expression.
I tried to do the substitution up to $k = 3$ but I failed to identify a recurring pattern. From the geometric intuition, though, we should have
$$ x_n \sim \cos(\theta) \quad \text{and} \quad y_n \sim \sin(\theta) \quad \text{as} \ n \to \infty $$
A lot of steps have been skipped in the original article, and somehow, the final result is as follows
$$ x_n = \sum_{k=0}^{\lfloor n/2 \rfloor}(-1)^k \bigg({n \atop 2k}\bigg) \bigg(1 - \frac{(\theta/n)^2}{2}\bigg)^{n-2k} \bigg(\frac\theta n\bigg)^{2k} \bigg(1 - \frac{(\theta/n)^2}{4}\bigg)^k $$
and
$$ y_n = \sum_{k=0}^{\lfloor n/2 \rfloor}(-1)^k \bigg({n \atop 2k+1}\bigg) \bigg(1 - \frac{(\theta/n)^2}{2}\bigg)^{n-2k-1} \bigg(\frac\theta n\bigg)^{2k+1} \bigg(1 - \frac{(\theta/n)^2}{4}\bigg)^{k+(1/2)} $$
In the limit as $n \to \infty$ and glossing over some convergence details, it can be shown that the two above expressions simplify to the power series of cosine and sine, respectively.
To me, it seems not so trivial to derive those two expressions. I like the concept, and I would like some help or guidance on what steps could have been used to get those two results.