0

Following the equation in Wikipedia, I've implemented it except that I have a small problem when evaluating it:

enter image description here

This is the resulting code just in case, I triple checked it but it just looks right to me:

x = Mathf.Pow(Mathf.Abs(Mathf.Cos(t)), 2.0f / n) * a * Mathf.Sign(Mathf.Cos(t));
y = Mathf.Pow(Mathf.Abs(Mathf.Sin(t)), 2.0f / n) * b * Mathf.Sign(Mathf.Sin(t));

I effectively get such paths when setting the value of n:

enter image description here

Here's the actual problem explained with two animated GIFs:

I evaluate t in a linear fashion like this:

enter image description here

When I set n to 1 so that it's losange-like, animation is mostly linear:

enter image description here

But when I set n to 5 so that it's square-like, there are abrupt changes:

enter image description here

Basically, what I'm looking for, is that when I evaluate t in a linear fashion, the resulting coordinates would not jump over certain points in the curve as it does in the animation shown above, i.e. a constantly smooth movement.

That said, I have no idea on how to achieve that if someone could provide some cues on how to.

Eric Cartman
  • 297
  • I don't understand at all what your animated gifs represent. What is the meaning of the coordinates axes (is it the first quadrant ?). What is the meaning of the color code, etc. – Jean Marie Apr 15 '23 at 06:31
  • 1
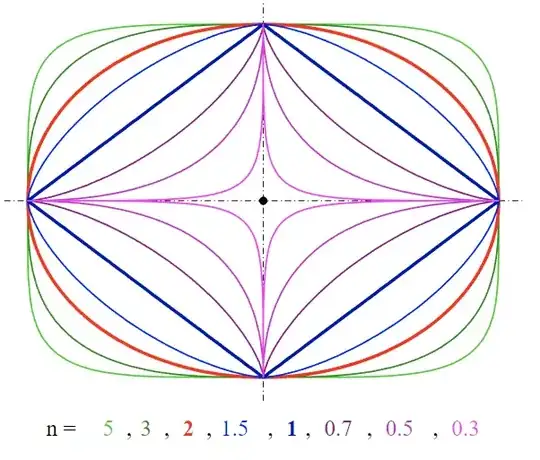
    In the second image, you can see the shape of the ellipse with different values of n, in the fourth image, when I evaluate t you can see that the middle of image follows a losange path, i.e. n is 1. In the last image, it's the same but for n of 5, i.e. a squarified shape. On both animations you can see that when I reach north/east/south/west, it spends very little time compared to other positions, i.e. it's not linear. When you plot this on a still image there's no problem as it's still; but in an animation it isn't. Hope it's clearer for you by now. – Eric Cartman Apr 15 '23 at 06:40
  • You might be looking for a constant path speed parameterization, i.e. something which gives you equal path length per unit of time. https://math.stackexchange.com/a/1123448/35416 discusses this for the case of the normal ellipse. Not sure whether any of that would be applicable for superellipses. If the purpose is animation I'd suggest some simple approximations. For small steps the direct distance between points and the path length between them would be very similar, with the former easier to compute. Using that you could use some gradient descent or so to find the $t$ for a desired distance. – MvG Apr 15 '23 at 20:45

0 Answers0