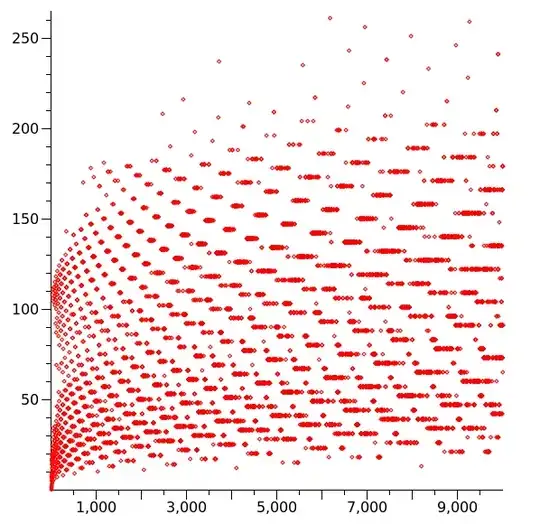
We define the Collatz stopping-time of an integer $n$ to be the number of iterations of the Collatz function on $n$ untill we reach $1$. A corollary of the Colatz conjecture is that this time is finite for all $n$.
This is a plot of the stopping-time for numbers up to $10^4$.
The plot seems to consist of a family of decreasing curves. Is there a known formula for these curves?