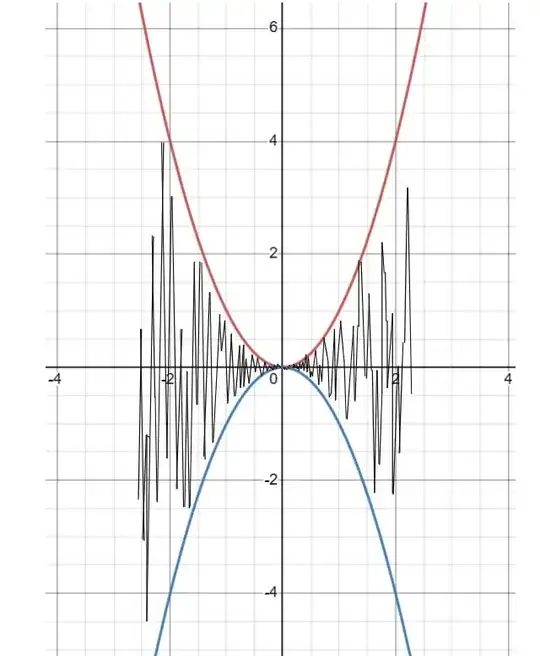
Motivation: The Weierstrass function is both nowhere differentiable and does not contain an interval on which it monotone (i.e. either increasing or decreasing).
If $\ f: \mathbb{R}\to\mathbb{R}\ $ is continuous, and there is no interval on which $\ f\ $ is monotone, then I believe it is still possible for there to be a point at which $\ f\ $ is differentiable. For example, some crazy Weierstrass-type function but changed so that it is bounded between the curves $y=x^2$ and $y=-x^2.$ Then since $f$ is continuous, $f(0)$ must be equal to $0,$ and also $f'(0)$ must be zero, so the derivative must exist at this point. I tried my best to represent this with the graph below, but my graph isn't great as technically it contains straight lines. It isn't supposed to contain straight lines: it is supposed to be a fractal as you keep zooming in like the Weierstrass function. Anyway, I believe my concept of counter-example is correct here.
However:
Is it true that, if $\ f: \mathbb{R}\to\mathbb{R}\ $ is continuous, and there is no interval on which $\ f\ $ is monotone, then there is no interval on which $\ f\ $ is differentiable?
I suspect the answer is yes. The contrapositive might be easier to prove, but I'm not sure how to go about doing so.