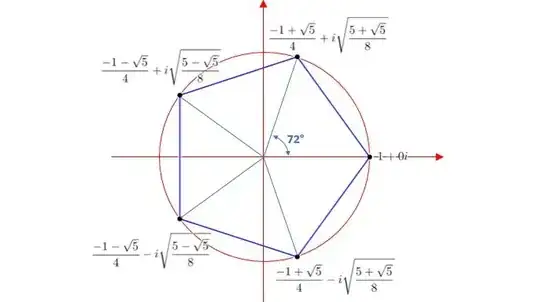
I have the following problem on one of my assignments:
find all five fifth roots of 32.
What I find interesting is how $\varphi$ is related to the real component of most of the solutions. My intuition points me towards the definition of $\varphi$, namely $\varphi$ = $\frac{\sqrt{5} + 1}{2}$
Here are the solutions: $2$, $0.618+0.951i$, $-1.618+1.176i$, $-1.618-1.176i$, $0.618-1.902i$
Four of the solutions have real component (of what seems to be) either $-\varphi$ or $\varphi - 1$. It is not just a coincidence to do with rounding, it is exactly equal to $-\varphi$ and $\varphi - 1$ out to 10 decimal places.
Is there some deeper relation that I am missing? I was shocked to get this answer.