The origin of $\pi$

Question

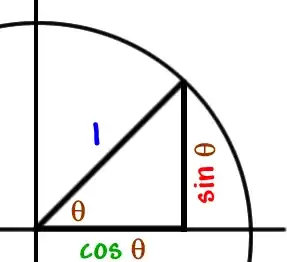
How was $\pi$ originally found? Was it originally found using the ratio of the circumference to diameter of a circle of was it found using trigonometric functions? I am trying to find a way to find the area of the circle without using $\pi$ at all but it seems impossible, or is it? If i integrate the circle I get: $$4\int_{0}^{1}\sqrt{1-x^{2}}dx=4\left [ \frac{\sin^{-1} x}{2}+\frac{x\sqrt{1-x^{2}}}{2} \right ]_{0}^{1}=\pi $$ But why does $\sin^{-1} 1=\frac{\pi }{2}$?

Is it at all possible to find the exact area of the circle without using $\pi$?

Answer 1

I don't know the exact origin of $\pi$ but you should not be able to find the exact area of the unit circle (your integral suggests you are finding this) without reference to $\pi$ since this is the exact area. You also could, of course, not write this number down exactly since $\pi$ is transcendental. You could approximate this number, and thus approximate the area of the unit circle, without reference to $\pi$. To do this in terms of the integral you could use a numerical approximation technique.

$\sin^{-1}(x)\neq \frac{\pi}{2}$ in general as you have written. But it is true for $x=1$. This can be seen by noting that on a unit circle $\sin(x)$ is simply the $y$ component of the point on the unit circle corresponding to angle $x$, measured from the positive $x$-axis, with centre at $(0,0)$ (I put a diagram to help visualize what I am saying). So at the point $(0,1)$ on the unit circle the $y$-component is $1$ and this corresponds to angle $\frac{\pi}{2}$.

Answer 2

I don't know the history behind $\pi$. But I can talk about how you thought you can find the exact value of $\pi$ using integrals and ended up back to $\pi$. This has to do with definitions. The definition of $\pi$ and trig functions are interrelated and the way you used it becomes circular. One way to define $\pi$ is by $4\int_{0}^{1}\sqrt{1-x^{2}}\,dx$ or $2\int_{-1}^{1}\sqrt{1-x^{2}}\,dx$ (same thing by symmetry). This integral cannot be "evaluated" by elementary functions like $f(x) = x^a$ where $a \in \mathbb{R}$. It can be "evaluated" using trigonometric functions because of how they are defined. One way of defining $\sin$ rigorously is theough an integral. We can define $$ \arcsin(x) = \int_0^x \frac{1}{\sqrt{1 - t^2}}\, dt $$ ($\sin$ is defined as the inverse of $\arcsin$ and extended to the whole real line so that it is periodic) With these definitions, and using the equation you wrote, we can derive that $\arcsin(1) = \frac{\pi}{2}$.

What I tried to show is that you can't get the exact area of a unit circle because you can't evaluate the integral in terms of elementary function (besides trig). So you can only define $\pi$ as that area and define a new functions ($\arcsin$ and $\sin$). The underlying reason is because $\pi$ is transcendental which means it is not a solution to any polynomial with integer coefficients. So its not just irrational, we can't express $\pi$ using radicals and other arithmetic operations and its not even a root of a polynomial.

However, you can get many series for $\pi$ which basically means you can write $\pi$ as the limit of a sequence of sums. You can do this for any real number (including transcendental): there is a sequence of rational numbers whose limit is that real number.

Note that there are other ways to define $\pi$ and trigonometric functions rigorously But the same kind of thing will happen.

Answer 3

You could look at the history of $\pi$.

The Egyptian version gives $20\sqrt{2}/9$, which gives an quadrant arc of $10$ around a square of edge $9$.

The values of $3$ and $3 \frac{17}{120}$ come from measurement.

The geometric approach is to compare diameter to circumference of a polygon $2^n3$. This is the usual approach to finding this number until fancy series come into play.

One method for calculating the area of a circle, is to suppose it is a polygon $p$ of edge $1$, and shortchord $s$. You then get circumference is $p$, and diameter is $2/\sqrt{4-s^2}$ and pi comes as $\frac p2\sqrt{4-s}$. When you double $p''=2p$, then $s'' = \sqrt{2+s}$.

The shortchord being the chrod forming a triangle with two edges. For the hexagon, the shortchord is $\sqrt{3}$, but you can start with the triangle, where the shortchord is $1$.

Since this is a triangle, one can calculate the area as $A = ps / 2\sqrt{4-s^2}$

Answer 4

One has to make a distinction between $\pi$ and it's value for Euclidean geometry, for example what is the value of $\pi$ on a sphere? If there are two formulas for circumference and area, why is the value of $\pi$ same in both of them? could there be other geometries where the value are not the same? or could value of $\pi=42$? $\pi$ in arbitrary metric spaces

Update: On a sphere $\pi$ is not unique! the good question from @MJD made me realise that : One of many definitions of $\pi$ is the ratio of circumference of the circle to it's radius. On a sphere a circle could be considered to having 2 redies, to see that draw a circle on the equator and draw another one parallel to the equator to the north or south of the first one. now ask yourself what is the radius of each circle on the sphere? the one on equator has two equal radius starting on either poles, but the other one has 2 unequal radius on the sphere. Now if every circle has 2 different radius on a sphere, it has 2 different ratios for it's ratio of radius to its circumference.

Answer 5

to answer at "Is it at all possible to find the exact area of the circle without using π?"

hello, $A=CR/2$

"How was π originally found?"

maybe Pythagore and euclide with a²+b²=c² found the area of squares. Then Archimede found $3+10/71<pi<3+1/7$