Each Iteration: Given a $[0,1]$ interval partitioned into sub-intervals $I_1\ldots,I_n$, choose $k\in[n]$ uniformly at random. Subdivide interval $I_k$ into two disjoint intervals of equal size.
Let $f(N)$ be the expected size of a smallest interval after iterating $N$ times, given an initial partition of only one part (the entire interval).
Here's the results for small $N$:
- $N=1: 1/2$ -- Parts have sizes: $\{\frac{1}{2}, \frac{1}{2}\}$
- $N=2: 1/4$ -- Parts have sizes: $\{\frac{1}{2}, \frac{1}{4}, \frac{1}{4}\}$
- $N=3: 1/6 = (1/3)(1/4) + (2/3)(1/8)$
- $N=4: 5/48 = (1/3)(1/8) + (2/3)((2/4)(1/16)+(1/4)(1/8)+(1/4)(1/8))$
- $N=5: 19/240 = (2/3)((2/4)((2/5)(1/32)+(3/5)(1/16))+(1/4)((4/5)(1/16)+(1/5)(1/8))+(1/4)((2/5)(1/16)+(3/5)(1/8)))+(1/3)((2/5)(1/16)+(3/5)(1/8))$
Explanation for the N=3 case: If the interval of size 1/2 is chosen to be subdivided (there is a 1/3rd chance of this happening) then the smallest part has size 1/4. Otherwise the smallest part has size 1/8.
This problem feels solvable via induction/recursion. I haven't put any effort in that direction yet. I've not seen this problem elsewhere, and am posting it just because I think someone might find it fun to solve.
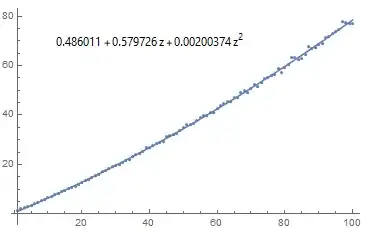
I've simulated it for N=1 up to 100. It appears to resemble $N^{-2}$ so I plotted $1/\sqrt{f(N)}$ and the best fit parabola. It's a decent match but there's still a small quadratic term indicating some linear component to $1/f(N)$. Here's the plot:
This $1/N^2$ behavior matches with the results of similar questions. Maybe this question can reduce to one of these already solved:
- Average minimum distance between $n$ points generate i.i.d. with uniform dist.
- Expected minimum distance for $n$ points on a circle
An important difference between those questions and this one is that the intervals in this question are equally likely to be subdivided when iterating.