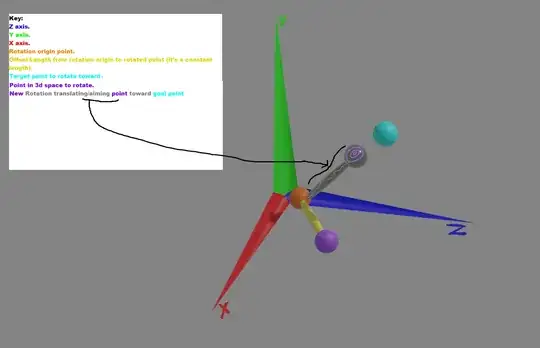
I have a point in a 3D space rotated by a quaternion. The point has a fixed length from the rotation itself (shown in image). What I'm trying to achieve is to rotate my point towards a goal position represented here by another point. if I just have the target position, the position of the rotated point, the length of the offset form my rotation origin, and the rotation (represented by a quaternion) and the rotations position (see orange sphere in picture) is it possible to find a quaternion to aim/point/translate my point towards the target position/point?
-
Did I understand you correctly? You are looking for a quaternion that, when multiplied by the purple dot's quaternion representation, becomes the blue dot? – Kevin Dietrich Mar 22 '23 at 20:23
-
Would you also tell us your ideas and attempted solutions so that we can really help and not just solve the task for you. – Kevin Dietrich Mar 22 '23 at 20:24
-
maybe that this answer is what you are searching : https://math.stackexchange.com/questions/1569215/given-a-start-point-in-3d-and-a-quaternion-and-length-to-point-b-can-you-find-po/1572193#1572193 – Emilio Novati Mar 23 '23 at 10:49
1 Answers
Let's say that the point around which to rotate ${\color{Orange} o}$ has coordinates $\left( {\color{Orange} o_{{\color{Red} x}}},\, {\color{Orange} o_{{\color{Green} y}}},\, {\color{Orange} o_{{\color{Blue} z}}} \right)$, that the point to rotate ${\color{Purple} v}$ has the coordinates $\left( {\color{Purple} v_{{\color{Red} x}}},\, {\color{Purple} v_{{\color{Green} y}}},\, {\color{Purple} v_{{\color{Blue} z}}} \right)$ and thus the Quaternion Representation ${\color{Purple} v} ~\widehat{=} \begin{pmatrix} {\color{Purple} v_{{\color{Black} w}}}\\ {\color{Purple} v_{{\color{Red} x}}}\\ {\color{Purple} v_{{\color{Green} y}}}\\ {\color{Purple} v_{{\color{Blue} z}}} \end{pmatrix} \widehat{=}~ {\color{Purple} v_{{\color{Black} w}}} + {\color{Purple} v_{{\color{Red} x}}} \cdot \mathrm{i} + {\color{Purple} v_{{\color{Green} y}}} \cdot \mathrm{j} + {\color{Purple} v_{{\color{Blue} z}}} \cdot \mathrm{k}$ has, that the point is rotated to ${\color{Purple} v_{\text{rotaded}}}$ has coordinates $\left( {\color{Purple} v_{\text{rotaded},\, {\color{Red} x}}},\, {\color{Purple} v_{\text{rotaded},\, {\color{Green} y}}},\, {\color{Purple} v_{\text{rotaded},\, {\color{Blue} z}}} \right)$ and thus has the quaternion representation ${\color{Purple} v} ~\widehat{=} \begin{pmatrix} {\color{Purple} v_{\text{rotaded},\, {\color{Black} w}}}\\ {\color{Purple} v_{\text{rotaded},\, {\color{Red} x}}}\\ {\color{Purple} v_{\text{rotaded},\, {\color{Green} y}}}\\ {\color{Purple} v_{\text{rotaded},\, {\color{Blue} z}}} \end{pmatrix} \widehat{=}~ {\color{Purple} v_{\text{rotaded},\, {\color{Black} w}}} + {\color{Purple} v_{\text{rotaded},\, {\color{Red} x}}} \cdot \mathrm{i} + {\color{Purple} v_{\text{rotaded},\, {\color{Green} y}}} \cdot \mathrm{j} + {\color{Purple} v_{\text{rotaded},\, {\color{Blue} z}}} \cdot \mathrm{k}$ and that the target point ${\color{Cyan} a}$ has the coordinates $\left( {\color{Cyan} a_{{\color{Red} x}}},\, {\color{Cyan} a_{{\color{Green} y}}},\, {\color{Cyan} a_{{\color{Blue} z}}} \right)$ and thus has the quaternion representation ${\color{Cyan} a} ~\widehat{=} \begin{pmatrix} {\color{Cyan} a_{{\color{Black} w}}}\\ {\color{Cyan} a_{{\color{Red} x}}}\\ {\color{Cyan} a_{{\color{Green} y}}}\\ {\color{Cyan} a_{{\color{Blue} z}}} \end{pmatrix} \widehat{=}~ {\color{Cyan} a_{{\color{Black} w}}} + {\color{Cyan} a_{{\color{Red} x}}} \cdot \mathrm{i} + {\color{Cyan} a_{{\color{Green} y}}} \cdot \mathrm{j} + {\color{Cyan} a_{{\color{Blue} z}}} \cdot \mathrm{k}$.
Since the only thing that differentiates ${\color{Purple} v_{\text{rotaded}}}$ and ${\color{Cyan} a}$ is the absolute distance to ${\color{Orange} o}$, which we can normalize: $$ \begin{align*} {\color{Purple} v_{\text{rotaded}}} &= ||{\color{Purple} v_{\text{rotaded}}}|| \cdot {\color{Purple} v_{\text{rotaded},\, 0}}\\ {\color{Cyan} a} &= ||{\color{Cyan} a}|| \cdot {\color{Cyan} a_{0}}\\ {\color{Purple} v_{\text{rotaded},\, 0}} &= {\color{Cyan} a_{0}}\\ ||{\color{Purple} v}|| &= ||{\color{Purple} v_{\text{rotaded}}}||\\ {\color{Purple} v_{\text{rotaded}}} &= ||{\color{Purple} v}|| \cdot {\color{Cyan} a_{0}}\\ {\color{Purple} v_{\text{rotaded}}} &= ||{\color{Purple} v}|| \cdot \frac{{\color{Cyan} a}}{||{\color{Cyan} a}||}\\ \end{align*} $$
Thus, the target point ${\color{Purple} v_{\text{rotaded}}}$ in the form of the point to be drawn ${\color{Cyan} a}$ and the origin point can be represented ${\color{Purple} v}$.
The easiest way I could think of to do this would be to bring the orange dot to the center of the coordinate system and then use the classic formula for $3$D rotation of a vector via quaternions.
Then we can take ${\color{Orange} o}$ as the coordinate origin by subtracting the components of ${\color{Orange} o}$ from the points and thus moving everything relative to to the center: $$ \begin{align*} \mathrm{v} &= \begin{pmatrix} 0\\ {\color{Purple} v_{{\color{Red} x}}} - {\color{Orange} o_{{\color{Red} x}}}\\ {\color{Purple} v_{{\color{Green} y}}} - {\color{Orange} o_{{\color{Green} y}}}\\ {\color{Purple} v_{{\color{Blue} z}}} - {\color{Orange} o_{{\color{Blue} z}}} \end{pmatrix} \widehat{=} \left( {\color{Purple} v_{{\color{Red} x}}} - {\color{Orange} o_{{\color{Red} x}}} \right) \cdot \mathrm{i} + \left( {\color{Purple} v_{{\color{Green} y}}} - {\color{Orange} o_{{\color{Green} y}}} \right) \cdot \mathrm{j} + \left( {\color{Purple} v_{{\color{Blue} z}}} - {\color{Orange} o_{{\color{Blue} z}}} \right) \cdot \mathrm{k}\\ \mathrm{v}_{\text{rotaded}} &= \begin{pmatrix} 0\\ {\color{Purple} v_{\text{rotaded},\, {\color{Red} x}}} - {\color{Orange} o_{{\color{Red} x}}}\\ {\color{Purple} v_{\text{rotaded},\, {\color{Green} y}}} - {\color{Orange} o_{{\color{Green} y}}}\\ {\color{Purple} v_{\text{rotaded},\, {\color{Blue} z}}} - {\color{Orange} o_{{\color{Blue} z}}} \end{pmatrix} \widehat{=} \left( {\color{Purple} v_{\text{rotaded},\, {\color{Red} x}}} - {\color{Orange} o_{{\color{Red} x}}} \right) \cdot \mathrm{i} + \left( {\color{Purple} v_{\text{rotaded},\, {\color{Green} y}}} - {\color{Orange} o_{{\color{Green} y}}} \right) \cdot \mathrm{j} + \left( {\color{Purple} v_{\text{rotaded},\, {\color{Blue} z}}} - {\color{Orange} o_{{\color{Blue} z}}} \right) \cdot \mathrm{k}\\ \mathrm{v}_{\text{rotaded}} &= \begin{pmatrix} 0\\ \frac{||{\color{Purple} v}||}{||{\color{Cyan} a}||} \cdot {\color{Cyan} a_{{\color{Red} x}}} - {\color{Orange} o_{{\color{Red} x}}}\\ \frac{||{\color{Purple} v}||}{||{\color{Cyan} a}||} \cdot {\color{Cyan} a_{{\color{Green} y}}} - {\color{Orange} o_{{\color{Green} y}}}\\ \frac{||{\color{Purple} v}||}{||{\color{Cyan} a}||} \cdot {\color{Cyan} a_{{\color{Blue} z}}} - {\color{Orange} o_{{\color{Blue} z}}} \end{pmatrix} \widehat{=} \left( \frac{||{\color{Purple} v}||}{||{\color{Cyan} a}||} \cdot {\color{Cyan} a_{{\color{Red} x}}} - {\color{Orange} o_{{\color{Red} x}}} \right) \cdot \mathrm{i} + \left( \frac{||{\color{Purple} v}||}{||{\color{Cyan} a}||} \cdot {\color{Cyan} a_{{\color{Green} y}}} - {\color{Orange} o_{{\color{Green} y}}} \right) \cdot \mathrm{j} + \left( \frac{||{\color{Purple} v}||}{||{\color{Cyan} a}||} \cdot {\color{Cyan} a_{{\color{Blue} z}}} - {\color{Orange} o_{{\color{Blue} z}}} \right) \cdot \mathrm{k}\\ \mathrm{a} &~= \begin{pmatrix} 0\\ {\color{Cyan} a_{{\color{Red} x}}} - {\color{Orange} o_{{\color{Red} x}}}\\ {\color{Cyan} a_{{\color{Green} y}}} - {\color{Orange} o_{{\color{Green} y}}}\\ {\color{Cyan} a_{{\color{Blue} z}}} - {\color{Orange} o_{{\color{Blue} z}}} \end{pmatrix} \widehat{=}~ \left( {\color{Cyan} a_{{\color{Red} x}}} - {\color{Orange} o_{{\color{Red} x}}} \right) \cdot \mathrm{i} + \left( {\color{Cyan} a_{{\color{Green} y}}} - {\color{Orange} o_{{\color{Green} y}}} \right) \cdot \mathrm{j} + \left( {\color{Cyan} a_{{\color{Blue} z}}} - {\color{Orange} o_{{\color{Blue} z}}} \right) \cdot \mathrm{k}\\ \end{align*} $$
We can apply this to the standard formula for quaternion rotation $\mathrm{v}_{\text{rotated}} = \mathrm{q} \cdot \mathrm{v} \cdot \overline{\mathrm{q}}$ and get:
$$ \begin{align*} \begin{pmatrix} 0\\ \frac{||{\color{Purple} v}||}{||{\color{Cyan} a}||} \cdot {\color{Cyan} a_{{\color{Red} x}}} - {\color{Orange} o_{{\color{Red} x}}}\\ \frac{||{\color{Purple} v}||}{||{\color{Cyan} a}||} \cdot {\color{Cyan} a_{{\color{Green} y}}} - {\color{Orange} o_{{\color{Green} y}}}\\ \frac{||{\color{Purple} v}||}{||{\color{Cyan} a}||} \cdot {\color{Cyan} a_{{\color{Blue} z}}} - {\color{Orange} o_{{\color{Blue} z}}} \end{pmatrix} &\widehat{=} \begin{pmatrix} q_{w}\\ q_{{\color{Red} x}}\\ q_{{\color{Green} y}}\\ q_{{\color{Blue} z}} \end{pmatrix} \cdot \begin{pmatrix} 0\\ {\color{Purple} v_{{\color{Red} x}}} - {\color{Orange} o_{{\color{Red} x}}}\\ {\color{Purple} v_{{\color{Green} y}}} - {\color{Orange} o_{{\color{Green} y}}}\\ {\color{Purple} v_{{\color{Blue} z}}} - {\color{Orange} o_{{\color{Blue} z}}} \end{pmatrix} \cdot \begin{pmatrix} q_{w}\\ -q_{{\color{Red} x}}\\ -q_{{\color{Green} y}}\\ -q_{{\color{Blue} z}} \end{pmatrix}\\ \begin{pmatrix} 0\\ \frac{||{\color{Purple} v}||}{||{\color{Cyan} a}||} \cdot {\color{Cyan} a_{{\color{Red} x}}} - {\color{Orange} o_{{\color{Red} x}}}\\ \frac{||{\color{Purple} v}||}{||{\color{Cyan} a}||} \cdot {\color{Cyan} a_{{\color{Green} y}}} - {\color{Orange} o_{{\color{Green} y}}}\\ \frac{||{\color{Purple} v}||}{||{\color{Cyan} a}||} \cdot {\color{Cyan} a_{{\color{Blue} z}}} - {\color{Orange} o_{{\color{Blue} z}}} \end{pmatrix} &\widehat{=} \begin{pmatrix} \cos\left( \frac{\varphi}{2} \right)\\ q_{{\color{Red} x}}\\ q_{{\color{Green} y}}\\ q_{{\color{Blue} z}} \end{pmatrix} \cdot \begin{pmatrix} 0\\ {\color{Purple} v_{{\color{Red} x}}} - {\color{Orange} o_{{\color{Red} x}}}\\ {\color{Purple} v_{{\color{Green} y}}} - {\color{Orange} o_{{\color{Green} y}}}\\ {\color{Purple} v_{{\color{Blue} z}}} - {\color{Orange} o_{{\color{Blue} z}}} \end{pmatrix} \cdot \begin{pmatrix} \cos\left( \frac{\varphi}{2} \right)\\ -q_{{\color{Red} x}}\\ -q_{{\color{Green} y}}\\ -q_{{\color{Blue} z}} \end{pmatrix}\\ \end{align*} $$
So what you are looking for is probably the quaternion $q = q_{w} + q_{{\color{Red} x}} \cdot \mathrm{i} + q_{{\color{Green} y}} \cdot \mathrm{j} + q_{{\color{Blue} z}} \cdot \mathrm{k}$ where $\varphi$ is the angle between ${\color{Cyan} a}$ and ${\color{Purple} v}$ to ${\color{Orange} o}$.
- 1,862