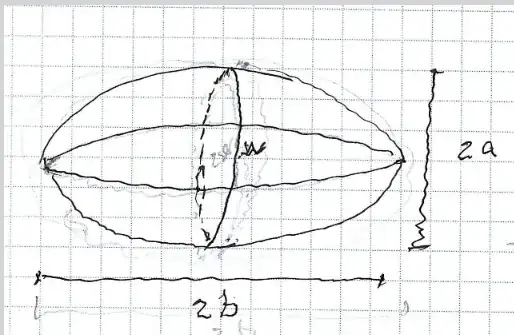
I'm an artist trying to sculpt shapes that I would describe as ellipsoids. I am wanting to sew together fabric to form these shapes, and although I know the dimensions of the ellipsoid I want to form, I don't know how to calculate the curvature of the pieces of fabric so they come together to form the ellipsoid (similar to gores on a globe).
For a sphere, I found the formula for the edges of the fabric to be: y = +/- R (pi/N) cos(x/R). N is the amount of gores, and x is the angular height. Source: https://www.themathdoctors.org/making-a-sphere-from-flat-material/?unapproved=21662&moderation-hash=f9644b82fc5759e707821810bd9753e8#comment-21662
But I'm not sure how to translate this formula into elliptical terms. The ellipsoid I'm trying to form has radii of 4.5 and 2.75 in. Does anyone have any suggestions, or know where I could turn to study this more?