Integral $\int_0^\infty\frac{dx}{\sqrt{1+\exp\left(\frac\pi2\left(x^2-\frac1{x^2}\right)\right) }}=\sqrt{\frac\pi2}$

Question

Someone posted the integral on a local chat group $$ \int_0^\infty\frac{dx}{\sqrt{1+\exp\left(\dfrac\pi2\left(x^2-\dfrac1{x^2}\right)\right) }}=\sqrt{\frac\pi2} $$ It is interesting that the integrand is quite messy but the result is neat.

Using CAS, I checked that the integral holds with high precision.

The first thing that came into my mind was the Glasser's master theorem, but it is not in an acceptable form. I also tried substituting $\dfrac{x^4-1}{2x^2}=t$ but the integral becomes even worse. $$ \int_{-\infty}^\infty\frac{\sqrt{\sqrt{t^2+1}+t}}{\sqrt{e^{\pi t}+1} \sqrt{t^2+1}}dt=\sqrt{2\pi} $$

Are there any ways to work out the integral? Or perhaps there is an approach to find the result magically?

Any help would be appreciated.

Answer 1

The integral is somehow nontrivial. I would proceed as follows.

OP's second attempt seems to be on the right track (at least for my approach). Denote the integral as $I$, substitute $\dfrac{x^4-1}{2x^2}=t$ so that $$ I=\int_0^\infty\frac{dx}{\sqrt{1+\exp\left(\dfrac\pi2\left(x^2-\dfrac1{x^2}\right)\right) }}=\frac12\int_{-\infty}^\infty\frac{\sqrt{\sqrt{t^2+1}+t}}{ \sqrt{t^2+1}}\frac{dt}{\sqrt{e^{\pi t}+1}} $$ The term $\dfrac{\sqrt{\sqrt{t^2+1}+t}}{ \sqrt{t^2+1}}$ reminds me of $\sin(\theta/2)$, so I came up with $$ \int_{-\infty }^{\infty } \frac{1}{\left(v^2-t\right)^2+1} dv=\Im \int_{-\infty }^{\infty } \frac{1}{v^2-t-i} dv =\Im\frac{\pi}{\sqrt{-t-i}} =\frac\pi{\sqrt2}\dfrac{\sqrt{\sqrt{t^2+1}+t}}{ \sqrt{t^2+1}} $$ and the integral becomes $$ I=\frac1{\sqrt2\pi}\int_{-\infty }^{\infty }\int_{-\infty}^\infty \frac{1}{\left(v^2-t\right)^2+1}\frac{1}{\sqrt{e^{\pi t}+1}}dvdt\\ =\frac1{\sqrt2\pi}\int_{-\infty }^{\infty }du\int_{-\infty}^\infty \frac{1}{\left(u^2(e^{\pi t}+1)-t\right)^2+1}dt \tag{$\ast$} $$ where $v=u\sqrt{e^{\pi t}+1}$.

Now consider the meromorphic function $f(z)=\dfrac1{u^2(e^{\pi z}-1)+z}$ and integrate on the rectangular contour $[-R,R]\times [-1,1]$. When $R\to\infty$, it is easy to see that the integrals on the vertical lines tend to vanish as $e^{-\pi R},\Re(z)=R\to\infty$ and $R^{-1}, \Re(z)=-R\to -\infty$. Meanwhile, the two on the horizontal line combines to get $$ \oint f(z)dz=\int_{-\infty}^\infty f(t-i)dt+\int^{-\infty}_\infty f(t+i)dt=2i\int_{-\infty}^\infty \frac{1}{\left(u^2(e^{\pi t}+1)-t\right)^2+1}dt $$ Thus, it suffice to investigate the location of the poles of $f(z)$. Though it normally has infinite poles on the complex plane, I claim that there's only one in the contour, namely $z=0$. To see this, let $z=\Re(z)+i \Im(z)=\xi+i\eta$ be a pole, then take the real and imaginary part $$ \cases{ u^2(e^{\pi\xi}\cos(\pi\eta)-1)+\xi=0 &(r)\\[5pt] u^2e^{\pi \xi}\sin(\pi \eta)+\eta=0 &(i) } $$ The two terms on the LHS of equation (i) always has the same sign when $-\pi<\eta<\pi$, so its only solution in the contour is $\eta=0$. Now equation (r) becomes $u^2(e^{\pi\xi}-1)+\xi=0$. It is easy to see that LHS is a monotonic function of $\xi$ and has a root $\xi=0$, so it is the only one, proving the claim.

By the residue theorem, $$ \oint f(z)dz=2\pi i\text{Res}[f(z),0]=\frac{2\pi i}{1+\pi u^2} $$ that is $$ \int_{-\infty}^\infty \frac{1}{\left(u^2(e^{\pi t}+1)-t\right)^2+1}dt=\frac{\pi}{1+\pi u^2} $$ plug this into $(\ast)$ $$ I=\frac1{\sqrt2\pi}\int_{-\infty}^\infty \frac{\pi}{1+\pi u^2}du=\sqrt{\frac{\pi}2} $$ as desired.

---

Update

I played around with my method and found more interesting result as one can plug any analytic function into $f(z)$ that keeps the contour integral neet. For example, $$ \int_0^\infty \frac{dx}{\sqrt{\cosh(x\sqrt{x^2+\pi})}}=\frac{\pi}{2\sqrt2} $$ Denote $t(x)=\dfrac{x^4-1}{2x^2}$ and $$ J_n=\int_0^\infty\frac{dx}{\sqrt{1+e^{\pi t(x)}}^{2n+1}}=\sqrt{\frac{\pi }{2}}\cdot[z^{-1}]\frac{1}{\sqrt{z \left(e^{ z}-1\right)} \left(1-e^{ z}\right)^n} $$ is always an rational multiple of $\sqrt{2\pi}$, like $$ J_1=\frac{3 }{8}\sqrt{2\pi}\quad J_2=\frac{65}{192}\sqrt{2\pi}\quad J_3=\frac{245 }{768}\sqrt{2\pi}\quad \cdots $$ One with more poles in the contour $$ \int_0^\infty\frac{\operatorname{sech}(\pi t(x))}{\sqrt{1+e^{\pi t(x)}}}dx=\sqrt{\sqrt{2}+1}-\sqrt{\frac{\pi }{2}} $$

However, now some of them seem to be trivial under @Sangchul Lee's brilliant approach.

Answer 2

Updated. Here is an alternative proof motivated by @Po1ynomial's wonderful observation. To begin with, we observe that, using the principal square root (corresponding to the choice of branch cut $(-\infty, 0]$),

Observation. For $x > 0$ and $t \in \mathbb{R}$, $$ t = \frac{x^2 - x^{-2}}{2} \qquad\iff\qquad x = \frac{\sqrt{t+i} + \sqrt{t-i}}{\sqrt{2}} = \operatorname{Re}\left(\sqrt{2}\sqrt{t + i} \right). $$

So, if we denote OP's integral by $I$, then

\begin{align*} I &= \frac{1}{\sqrt{2}} \int_{-\infty}^{\infty} \frac{1}{\sqrt{e^{\pi t} + 1}} \operatorname{Re} \biggl( \frac{1}{\sqrt{t + i}} \biggr) \, \mathrm{d}t \\ &= \frac{1}{\sqrt{2}} \lim_{T \to \infty} \operatorname{Re} \biggl( \int_{-T}^{T} \frac{1}{\sqrt{e^{\pi t} + 1}} \frac{1}{\sqrt{t + i}} \, \mathrm{d}t \biggr) \\ &= \frac{1}{\sqrt{2}} \lim_{T \to \infty} \operatorname{Re} \biggl( \int_{-T + i}^{T + i} \frac{1}{\sqrt{1 - e^{\pi z}} \sqrt{z}} \, \mathrm{d}z \biggr). \tag{$z = t + i$} \end{align*}

It is not hard to prove that $\sqrt{1 - e^{\pi z}}$ is analytic on the band $\mathbb{R} \times (0, 1]$. So, we can deform the contour $-T + i \to T + i$, without altering the value of the integral, to the piecewise contour (shown as the blue solid path below)

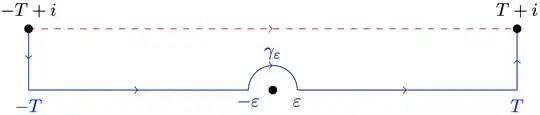
where $\gamma_{\varepsilon}(t) = \varepsilon e^{i(\pi - t)}$, $0 \leq t \leq \pi$, stands for the clockwise-oriented upper-semicircular arc of radius $\varepsilon \ll T$ about the origin. However, the contribution from the linear segment parts,

\begin{gather*} \underbrace{\int_{-T + i}^{-T} \frac{1}{\sqrt{1 - e^{\pi z}} \sqrt{z}} \, \mathrm{d}z}_{=\mathcal{O}(T^{-1/2})} + \underbrace{\int_{-T}^{-\varepsilon} \frac{1}{\sqrt{1 - e^{\pi x}} \cdot i \sqrt{x}} \, \mathrm{d}x}_{\text{pure imaginary}} \\ \hspace{3em} + \underbrace{\int_{\varepsilon}^{T} \frac{1}{i \sqrt{e^{\pi x} - 1} \sqrt{x}} \, \mathrm{d}x}_{\text{pure imaginary}} + \underbrace{\int_{T}^{T+i} \frac{1}{\sqrt{1 - e^{\pi z}} \sqrt{z}} \, \mathrm{d}z}_{=\mathcal{O}(e^{-\pi T/2} T^{-1/2})} \tag{*} \end{gather*}

is of the form $\text{[imaginary number]} + \mathcal{O}(T^{-1/2})$, hence its real part vanishes as $T \to \infty$. So, only the contribution from the circular arc $\gamma_{\varepsilon}$ survives under the limit as $T \to \infty$ and therefore

\begin{align*} I &= \frac{1}{\sqrt{2}} \operatorname{Re} \biggl( \int_{\gamma_{\varepsilon}} \frac{1}{\sqrt{1 - e^{\pi z}} \sqrt{z}} \, \mathrm{d}z \biggr) \\ &\quad \xrightarrow{\varepsilon \to 0^+} \frac{1}{\sqrt{2}} \operatorname{Re} \biggl( (-\pi i) \, \underset{z=0}{\mathrm{Res}} \, \frac{i}{z \sqrt{\frac{\exp(\pi z) - 1}{z}}} \biggr) = \bbox[color:navy; background:#F0F8FD; padding:10px; border:1px dotted navy;]{\sqrt{\frac{\pi}{2}}}. \end{align*}

---

Addendum. Write $ t(x) = \frac{\pi}{2}\left(x^2 - x^{-2} \right)$ for simplicity. Then numerical computations suggest the following identities:

\begin{align*} \int_{0}^{\infty} \frac{1}{\sqrt{1 + e^{t(x)}}} \, \mathrm{d}x &= \sqrt{\frac{\pi}{2}}, \tag{OP's integral} \\ \int_{0}^{\infty} \frac{e^{t(x)/4}}{\sqrt{1 + e^{t(x)}}} \, \mathrm{d}x &= \frac{\sqrt{\pi}}{2} \tag{2} \end{align*}

and

\begin{align*} \int_{0}^{\infty} \frac{1}{1 + e^{t(x)}} \, \mathrm{d}x &= -\frac{\zeta(\frac{1}{2})}{\sqrt{2}}, \tag{3} \\ \int_{0}^{\infty} \frac{e^{t(x)/4}}{1 + e^{t(x)}} \, \mathrm{d}x &= -\frac{\zeta(\frac{1}{2})}{2+\sqrt{2}}, \tag{4} \\ \int_{0}^{\infty} \frac{e^{t(x)/2}}{1 + e^{t(x)}} \, \mathrm{d}x &= -\frac{\zeta(\frac{1}{2})}{2+\sqrt{2}}, \tag{5} \\ \int_{0}^{\infty} \frac{1}{1 + e^{2t(x)}} \, \mathrm{d}x &= \frac{1}{\sqrt{2}} \biggl( 1 - \frac{\zeta(\frac{1}{2})}{2+\sqrt{2}} \biggr). \tag{6} \end{align*}

I was able to tackle some of these integrals using similar computations as above. For example, $\text{(2)}$ can be proved quite analogously as above, and $\text{(3)}$ boils down to

$$ \int_{0}^{\infty} \frac{1}{1 + e^{t(x)}} \, \mathrm{d}x = \frac{1}{\sqrt{2}} \int_{0}^{\infty} \frac{1}{\sqrt{x}} \left( \frac{1}{\pi x} - \frac{1}{e^{\pi x} - 1} \right) \, \mathrm{d}x, $$

which can be used to verify $\text{(3)}$. Instead of verifying everything by myself, however, I'll leave (4)--(6) to other users for fun!