5

According to the current Wikipedia article:

The Pareto principle or "80-20 rule" stating that 80% of outcomes are due to 20% of causes was named in honour of Pareto, but the concepts are distinct, and only Pareto distributions with shape value ($\alpha$) of $\log_4(5) \approx 1.16$ precisely reflect it.

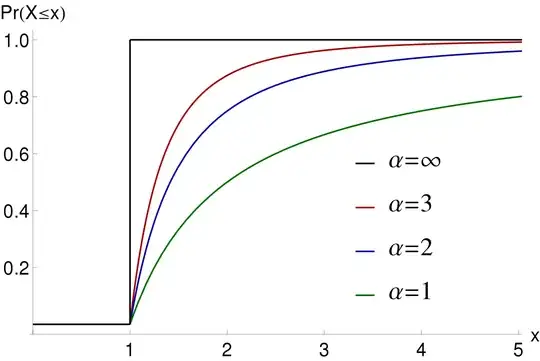
How do we interpret the Pareto distribution to make this connection?

I'm confused. The probability density function is

$$f_X(x) = \begin{cases} \displaystyle\frac{\alpha x_m^\alpha}{x^{\alpha + 1}} & x \geq x_m \\ 0 & x < x_m \\ \end{cases}$$

Here is a visualization of the corresponding cumulative density function for various $\alpha$, with $x_m = 1$.

The Pareto distribution.

For instance, suppose that 20% of landowners in an area own 80% of the land. I don't understand which part of the distribution corresponds to landowners and which part corresponds to land.

jskattt797
  • 1,731

1 Answers1

7

In your picture the values along the horizontal axis represent the amount of land owned by a randomly selected individual. The curve being plotted for a given $\alpha$ is a cumulative distribution function for amount of land owned, so the value of the curve at $x=t$ gives the fraction of individuals who own at most $t$ units of land.

If you are looking for the landowners who own 80% of the land, this is understood to mean those folks at the upper end of the wealth distribution. So you seek a threshold $t$ such that the total land owned by those who own $t$ or more units is $.8$ of the total land owned by everybody.

Notice that total land is not visible in the picture; to get total land you have to start with a histogram of land owned, and multiply each amount of land by the number of people who own that amount of land, then sum up. This total can also be computed using a density function, as described below.

Let $X$ be some measure of wealth, observed on a randomly selected individual, and suppose $X$ follows the Pareto distribution, with density $$ f_X(x) = \begin{cases} \displaystyle\frac{\alpha x_m^\alpha}{x^{\alpha + 1}} & x \geq x_m \\ 0 & x < x_m \\ \end{cases}.\tag1 $$ It is straightforward to calculate $E(X)=\frac\alpha{\alpha-1}x_m$, and for each $t>x_m$ you can verify that $$P(X>t)=\left(\frac {x_m}{t}\right)^\alpha\tag2$$ and $$E[XI(X>t)] = \int_t^\infty x f(x)\, dx=\frac\alpha{\alpha-1}\frac{x_m^\alpha}{t^{\alpha-1}}.\tag3$$

Now if the population consists of $n$ individuals then the total wealth in the population is $nE(X)$, while $nE[XI(X>t)]$ is the total wealth of those individuals whose wealth exceeds $t$. If we want the ratio of the latter to the former to be $0.8$, then we demand $$\left(\frac{x_m}t\right)^{\alpha-1}=\frac{n E[XI(X>t)]}{nE(X)}=0.8;\tag4$$ notice the population size conveniently cancels out. And if we want the fraction of individuals whose wealth exceeds $t$ to be $0.2$, then we demand $$\left(\frac{x_m}t\right)^\alpha=P(X>t)=0.2.\tag5$$ Taking the ratio of (5) to (4) yields $\frac {x_m}t=\frac14$. Plugging this into (5), this gives $$\left(\frac14\right)^\alpha =\frac15\iff 4^\alpha=5\iff \alpha=\log_4(5). $$

ADDED: As a consequence of (2), the wealthiest fraction $q$ the population are those whose wealth exceeds the threshold $t$ for which $(x_m/t)^\alpha=q$. Putting this into the left equation in (4), conclude that the share of total wealth for these folks is $q^{(\alpha-1)/\alpha}.$ If you seek a value for $\alpha$ such that the wealthiest fraction $q$ of the population owns fraction $p$ of the total wealth, then $\alpha$ satisfies $$p=q^{(\alpha-1)/\alpha}\iff\alpha = \frac{\log (1/q)}{\log (p/q)}.$$

grand_chat
  • 38,951
  • 1
    Note that (3) is not computing the expected wealth conditional on $X>t$. While it's meaningful to compute $E(X\mid X>t)$, using the quantity $nE(X\mid X>t)$ would be an overcount of the total wealth of the wealthy. Put another way, the total wealth of the wealthy equals (number of wealthy) $\times$ (expected wealth given wealthy) = $nP(X>t)\cdot E(X\mid X>t) = nE(XI(X>t))$. – grand_chat Mar 10 '23 at 15:04
  • Thank you so much. One more question: how do we interpret $x_m$ in this context? Seems like it's "the minimum wealth of any individual." I'd like to set $x_m$ to be $0$ (or even a negative number to account for debt), but the density function suggests that $x_m$ must be positive. – jskattt797 Mar 13 '23 at 04:42
  • 1
    @jskattt797 The parameter $x_m$ must be positive and is supposed to be the minimum possible value of $X$. This makes the Pareto distribution not ideal for modeling wealth. Indeed, later in the Wikipedia article is the comment "The Pareto distribution is not realistic for wealth for the lower end, however" – grand_chat Mar 13 '23 at 05:36