Geometric interpretation of integral $-\int\frac{1}{\sqrt{a+2bx-hx^{2}}}dx=\frac{1}{\sqrt{h}}\arccos\frac{b-hx}{\sqrt{b^{2}+ah}}$

Question

The following formula is given as "the familiar arc-cosine form" by Joos, in his Theoretical Physics. The German language original has $e$ in place of $h$.

$$-\int\frac{1}{\sqrt{a+2bx-hx^{2}}}dx=\frac{1}{\sqrt{h}}\arccos\left(\frac{b-hx}{\sqrt{b^{2}+ah}}\right)$$

The identity is used in the derivation of Kepler's laws. I have a couple of ways of deriving it. One of which is included as a screen-scrape.

Often such a "cookbook" formula is the product of a "standard recipe" in which the constants $a,b,h$ or $a,b,e$ have a meaning. Since this identity involves trigonometry, I am inclined to believe there is some geometric interpretation that would make the expression seem less mysterious. In particular, I am interested in a method that shows how it related to an ellipse, or a general second degree curve.

Is there a compelling geometric interpretation of the above integral formula?

All of the following is simply context, to show how the identity us used in treating the Kepler problem. The derivations are based on what is given by Joos. My derivation used a unit mass for most of the calculation. That is, for example, angular momentum becomes $\frac{\mathfrak{L}}{m}:=\vec{\mathcal{L}}.$

One method of producing the formula in question:

Read the right-hand side of equation in the lower left box from bottom to top. This is a result of an answer to a question about the same formula asked over six years ago.

Deriving the (un)familiar arc-cosine integral identity

The setup of the Kepler problem:

We assert the central force law of areas (Kepler's second law) as given.

$\dagger_1$ Conservation of energy. $\dagger_2$ Central force law of areas.

Putting the Kepler problem in the advertised form:

Integrating to obtain the expression for an elliptical orbit (Kepler's first law):

Obtaining the relationship of time to the semi-major axis (Kepler's third law):

Discussion of Quanto's answer(see my "answer" I can't get the image to display when added here)

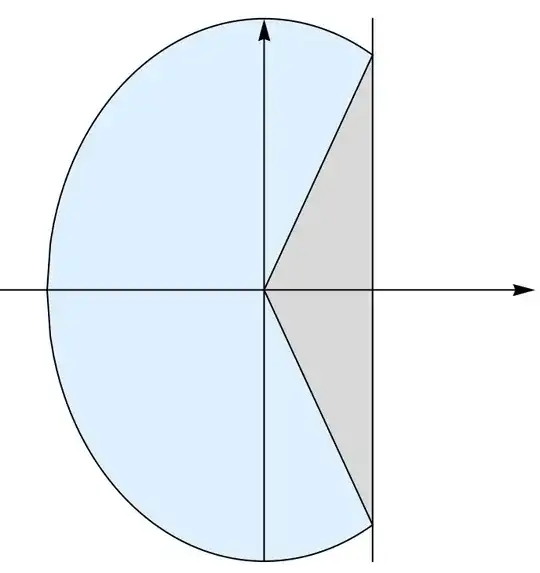
The filled region (blue $\cup$ gray) is

$$2\int_{-p}^{s}\sqrt{1-\frac{x^{2}}{p^{2}}}dx.$$

The gray triangle is

$$s\sqrt{1-\frac{s^{2}}{p^{2}}}.$$

Figuring out how to illustrate the second part may take a bit more time.

The most direct proof is likely to start from the integral representation $\cos^{-1} z=\int_x^1 \frac{1}{\sqrt{1-x^2}},dx$ and take $z$ to be the desired argument. Moreover, this integral representation has a simple geometric meaning (arc-length of circle as parametrized by horizontal coordinate). So one may be able to use this to reverse-engineer the geometry in the full case. — Semiclassical, Mar 04 '23 at 23:22
Comparing with Joos (and with robjohn's answer to the earlier problem), it seems like the denominator on the RHS should be $\sqrt{b^2 +ah}$. In addition, robjohn's result differs from Joos's by a minus sign in the argument of $\cos^{-1}$. But I'm uncertain if this makes a substantive difference within the context of Joos's calculation. — Semiclassical, Mar 05 '23 at 04:55
@Semiclassical Meh! That's Mathematica trying to be "helpfull." Copy as LaTex is not very reliable. I sincerely apologize for that. You will see that it is correct in the screen-scrape. I have now corrected the post (I hope). — Steven Thomas Hatton, Mar 05 '23 at 16:14
*Comment only, not towards an answer* Assuming $x$ is a coordinate on $x-$ axis and $\theta$ is the polar coordinate defined by the integral, $$\int\frac{-\sqrt {h}}{\sqrt{a+2bx-hx^{2}}}dx=\arccos\left(\frac{b-hx}{\sqrt{b^{2}+ah}}\right)= \theta $$ $$\frac{b-hx}{\sqrt{b^{2}+ah}}=\cos \theta $$ In polar coordinates $ x = r \cos \theta .$ Re-setting constants the curve assumes a form: $$ r= \frac{1-A \sec \theta}{B} $$ which is a Conchoid of Nicomedes rather than — Narasimham, Mar 06 '23 at 07:44

score 4 · Answer 1 · edited Mar 07 '23 at 15:23

For an ellipse of the form $\frac{x^2}{p^2} +{y^2}=1$, the following integral relationship holds

$$\int_{-p}^s \frac1{\sqrt{1-\frac{x^2}{p^2}}}dx = 2\int_{-p}^s {\sqrt{1-\frac{x^2}{p^2}}}dx -s \sqrt{1-\frac{s^2}{p^2}} $$ where the RHS is the area section of the ellipse on the left side of the vertical line $x=s$ minus the triangle area with the top vertex at the origin and the base $x=s$. Thus, the integral on the LHS is the left part of the elliptical area cut out by the two lines $y= \pm \frac {y\left(s\right)}sx$ starting from the origin.

Likewise, note that $\sqrt{a+2bx-hx^{2}} $ corresponds to the scaled ellipse $$h {\left(x-\frac bh \right)^2}+{y^2}=\frac{ah+b^2}{h} $$ with its center at $(\frac bh, 0)$ and left vertex at $ s_l = -\frac{\sqrt{ah+b^2}}h+\frac bh $. The corresponding integral

$$\int_{s_l}^{s}\frac{1}{\sqrt{a+2bx-hx^{2}}}dx =\int_{s_l}^{s}\frac{1}{\sqrt{\frac{ah+b^2}h-h\left(x-\frac bh\right)^2}}dx $$ has a similar geometric interpretation, i.e. the area cutout of the ellipse.

I'm working on this. I added a bit to my original post in response to your answer. — Steven Thomas Hatton, Mar 07 '23 at 15:35
Something very strange is happening with my graphics. The image is displayed in edit mode, but not in the post once it is committed. Same thing if I move the image to an answer. But it shows up in https://math.meta.stackexchange.com/q/35550/342834 — Steven Thomas Hatton, Mar 07 '23 at 15:59

Steven Thomas Hatton · Answer 2 · 2023-03-07T16:04:43.670

This is not an answer. I am just responding to the answer by Quanto. I was having trouble getting my graphic to appear in the original post. So I moved my comments here.

Discussion of Quanto's answer

This is what I believe the first part of the answer means.

I have no idea why my image is not displaying. This is another capture of the same graphic. Perhaps there is something strange going on with the data in the first one.