10

I am trying to learn math "from scratch" and started by reading an introductory logic textbook (A Concise introduction to logic) that did a great job explaining predicate logic. Among other things, proofs, that is, syntactic string manipulation where from a set of premises P, via a number of inference rules, a new statement, aka conclusion C, can be derived.

I am now profoundly stuck trying to make the leap to mathematical proofs. And here is where. The first introductory proof I saw looks like the following: Slide 42 from http://web.stanford.edu/class/archive/cs/cs103/cs103.1234/lectures/01/Lecture%20Slides.pdf

Slide 42 from here

But how does this connect to predicate logic? The predicate logic proofs begin with premises and here the theorem to be proven looks like the conclusion but no premises are given. Which I can understand: in propositional logic, a theorem is "a sentence that can be derived without premises" (ctrl + f for "theorem" here).

But where do I go from here?

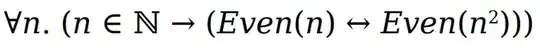
I can rewrite the theorem in predicate logic like the following enter image description here

But how can I go about proving it? The techniques in the textbook call for a sequence of conditional derivations and I would guess some universal instantiation or generalizations.

What am I missing to connect these 2 proofs? What is the link between a predicate logic proof and a math proof written in English?

I see that there is a square function involved that can be thought of as a relation (a form of predicate) and Even(x) is also a predicate, but aside from that i see no clues.

The math proof almost feels like a different underlying language and the predicate logic is like its skeleton that can not really be used here. Is that a valid notion?

Proving in math almost feels like using rules of arithmetic to get a matching definition while proving in predicate logic is more about producing a new string from the existing ones.

I see how this is a lot of thoughts pointing in potentially different directions but I am hoping that someone more experienced could notice/relate to the struggle and point me in the right direction.

Thank you everyone!

I believe my question is similar to the mathematical proof vs. first-order logic deductions but I did not find anything to answer my particular example.

boinka
  • 145
  • 8
  • I haven't read this in detail but you definitely don't want to read and write contemporary mathematics in pure FOL or whatever. No way. Even basics of any subject would become unreadable – FShrike Feb 26 '23 at 21:44
  • You have to define even. Lean suggests def even (n : ℕ) : Prop := ∃ m, n = 2 * m – Henry Feb 26 '23 at 21:53
  • @FShrike I do not have the objective to define all the maths, instead i want to know how to connect it. – boinka Feb 26 '23 at 22:05
  • 1
    Halmos quote: The symbolism of formal logic is indispensable in the discussion of the logic of mathematics, but used as a means of transmitting ideas from one mortal to another it becomes a cumbersome code. The author had to code his thoughts in it (I deny that anybody thinks in terms of ∃, ∀, ∧, and the like), and the reader has to decode what the author wrote; both steps are a waste of time and an obstruction to understanding. Symbolic presentation, in the sense of either the modern logician or the classical epsilontist, is something that machines can write and few but machines can read. – Pedro Feb 26 '23 at 23:22
  • The rewritten statement is not true because it says: “if n is a natural number then it must be even which is another way of saying that its square is even”. I would write it to say: “if n is a natural number which is also even that means it’s square is even”: $(\underbrace{n \in \Bbb N}{\text{n is natural}}\underbrace{\land}{\text{and}} \underbrace{\frac n2 \in \Bbb N}{\text{n is even}})\underbrace{\rightarrow}{\text{implies}} \underbrace{\frac{n^2}{2} \in \Bbb N}_{n^2\text{ is even}}$ – WindSoul Feb 27 '23 at 02:29
  • Learning logic before math is like trying to learn language before opening your eyes and looking at the world. – DanielV Feb 27 '23 at 03:40
  • @DanielV That reminds me of the quote "Learning model-theory before abstract algebra..." – Vivaan Daga Feb 27 '23 at 06:28
  • Also, this is rather tangential, but if you really want to learn about foundations, I would learn it from a mathematcian not a philosopher. – Vivaan Daga Feb 27 '23 at 06:41
  • 2
    @WindSoul Your definition of even seems to require division, which is a complicated subject among the natural numbers since in many cases $\frac n2$ is not defined at all – Henry Feb 27 '23 at 09:27
  • @Henry, I am thinking that $\frac n2$ is defined as natural even number via Euclid’s remainder algorithm determination of a zero remainder via subsequent subtraction of 2 from the result of previous subtraction (of 2) from n. – WindSoul Feb 27 '23 at 15:48
  • The key point is "generalization": if a property hold for a number $n$ whatever, then it hold for every number. – Mauro ALLEGRANZA Feb 28 '23 at 07:54
  • Also found this answer relevant: https://math.stackexchange.com/questions/3370383/what-is-the-difference-between-formal-logic-and-proofs – boinka Mar 03 '23 at 01:13

4 Answers4

8

I think what you call a "math proof" is best described as an argument that will convince another person of the truth of a particular mathematical assertion about numbers or shapes or other structures mathematicians define and think about.

Those arguments are written in ordinary English (or other natural language) augmented by some mathematical symbols as appropriate.

The level of detail required to be convincing depends on the amount of mathematical knowledge the reader and the writer share.

There is no need to translate those arguments into formal statements in predicate logic. In fact, that is usually a bad idea since it can obscure the mathematical meaning you want to convey.

My personal opinion is that focusing on predicate logic in a first course in "how to write proofs" is counterproductive. I tell my students in that course that a good proof is one that convinces me that you have convinced yourself for good reasons.

Ethan Bolker
  • 95,224
  • 7
  • 108
  • 199
  • Thank you for the swift reply, Ethan. Never came across the opinion that it might be counterproductive to first study logic as i thought it is the foundation of it all. (Followed by some set theory, then abstract algebra, than arithmetic). Could you elaborate on what you think the relationship between predicate logic and math is then. By math, I guess, I would mean arithmetic and basic algebra to keep it in the context of this example proof – boinka Feb 26 '23 at 22:09
  • 2
    Predicate logic is a formal system that tries to encapsulate the intuitive idea of "proof from axioms". Mathematicians interested in that formality study it using the kinds of arguments you call "math proof" - they don't write proofs about predicate logic in predicate logic. To do good mathematics about arithmetic and basic algebra and pretty much all of the undergraduate curriculum you need never study predicate logic for its own sake at all. Some of the ideas and notations there (quantification, sets corresponding to propositions) are useful. – Ethan Bolker Feb 27 '23 at 02:32
  • 2
    Moreover, you don't learn mathematics by starting with the foundations, so logic, then set theory, then abstract algebra, then arithmetic. Number theory starts with the properties of numbers, whose nature is intuitively clear. In time you see that there are abstractions at work that lead you to invent abstract algebra. Set theory can help a bit there, so you learn some of that. As you dig in, you find that you must shore up foundations in logic. But you don't start with the foundations. If that were necessary how would Gauss and Archimedes have done what they did? – Ethan Bolker Feb 27 '23 at 02:41
  • Instead of thinking of logic coming "before" math, think of logic being just another field of math. – Vivaan Daga Feb 27 '23 at 07:12
  • The classic argument of "all men are mortal; soc is a man; therefore soc is mortal" can be abstracted to predicate logic and look like: {∀x Man(x)->Mortal(x); ∀x Socrates(x)->Man(x)} therefore {∀x Socrates(x) -> Mortal(x)}. I was wondering if there is a way to perform the say abstraction on math proofs such as the one above or is there something that I am missing in that makes this abstraction impossible? It looks like the actual proof in math is operating at a level of detail that is too granular for predicate logic to capture. Is that the right intuition? – boinka Mar 01 '23 at 01:26
  • @boinka That kind of abstraction is often possible - but there is no good reason for everyday mathematicians to do so. The argument in English for Socrates' mortality is much more understandable than its formalization. – Ethan Bolker Mar 01 '23 at 01:32
  • Ethan,.I completely agree, but.I asked my question because I wanted to understand how you the 2 connect. That is, how can predicate logic be used to describe a mental proof in English – boinka Mar 03 '23 at 14:32
4

I like to think of mathematical proofs as convincing the audience that there is a syntactic string manipulation type proof of the statement, and to give guidance as to how to construct that proof. For the example proof you give, you can start with:

$\forall n: even(n) \implies \exists k: n = 2k$, the definition of $even(n)$

and then use that $\forall a: \forall b: a = b \implies a^2 = b^2$ (which maybe you're going to want to prove from even simpler foundations) and then some tricks with the quantifiers to get:

$\forall n: even(n) \implies \exists k: n^2 = (2k)^2$

Depending on the exact syntactic system you're working in, the exact process of unpacking this proof-in-words will be slightly different, but the template will be the same: just follow the steps in the proof-in-words.

If you're interested in purely syntactic proofs, here's a proof of a similar fact at metamath: https://us.metamath.org/mpeuni/mulsucdiv2z.html

TomKern
  • 2,977
  • So the two premises would be (1) ∀n:even(n)⟹∃k:n=2k) and (2) ∀a:∀b: a=b⟹a^2=b^2. and then the syntactic rules of logic and arithmetic will yield the ∀n:even(n)⟹∃k:n2=(2k)2 as the conlcusion? – boinka Mar 01 '23 at 01:18
2

Nobody mentioned proof assistants: Coq, Agda, Idris, Isabelle, etc.
https://en.m.wikipedia.org/wiki/Proof_assistant

They show that, yes, it is possible to completely formalize a proof to the point that it can be mechanically checked, and that some mathematicians actually did it for some very complex proofs (in Coq: the four color theorem; the Feit-Thompson theorem).

But they also show that using such perfectly formal languages is greatly unproductive, requires a lot of specific training, and produces proofs that are a lot less readable than plain english proofs. Also, they put forward a lot of differences and subtleties between various logics and type theories, that non-specialists (i.e. mathematicians that are not logic specialists) would rather ignore.

Some mathematicians like Voevodsky have concluded - after some bitter personal experience - that long, complex proofs are too error-prone, and must be checked by computarized means. But Voevodsky was also negative about the usability of predicate logic for computerized proofs, felling that predicate logic was too low-level. That would be like designing complex software in Assembly language. This was the main driver of his researches after 2000.
https://www.ias.edu/ideas/2014/voevodsky-origins

As a personal taste, I like epsilon-delta kinds of proofs. Difference between continuity and uniform continuity is much clearer when fully written with quantifiers, than in plain English. But that's somewhat a narrow case.

Jean-Armand Moroni
  • 5,632
1

Adding to Ethan's answer and specifically addressing your questions:

The predicate logic proofs begin with premises, and here the theorem to be proven looks like the conclusion but no premises are given. Which I can understand: in propositional logic, a theorem is "a sentence that can be derived without premises".

A mathematical theorem is premised ultimately on mathematical axioms and an interpretation of its mathematical symbols. The axiom system and background toolkit (definitions, rules, laws, lemmas, other theorems) is tacit. This is in contrast to pure theorems, which are logical validities/truths; here, the adjective 'logical' is not merely indicating that the statement is logically derivable, but that it is true regardless of interpretation.

Proving in math almost feels like using rules of arithmetic to get a matching definition

Quibble: proofs derive results, not definitions.

$$\forall n.\,(n\in\mathbb N\to(\text{Even}(n)\leftrightarrow\text{Even}(n^2)))\tag0$$

Correction: see $(2)$ below.

What is the link between a predicate logic proof and a math proof written in English?

Proof: Pick an arbitrary even integer $n.$ We need to show that $n²$ is even.

Here, the author means that $$(n\in\mathbb Z \land \text{Even}(n))\to \text{Even}(n^2)\tag1$$ logically implies $$n\in\mathbb Z\to(\text{Even}(n)\to\text{Even}(n^2)),$$ and that invoking universal generalisation then gives the required result $$\forall n\;(n\in\mathbb Z\to(\text{Even}(n)\to\text{Even}(n^2))).\tag2$$ So far, no mathematics has been performed yet.

Since $n$ is even, there is some integer $k$ such that $n = 2k.$

Here, the author is using multiplication, an arithmetical operation, and invoking the definition of "even number", that is, what it means for the predicate Even$(n)$ to be true/false.

This means that $n^2 = (2k)^2= 4k^2 = 2(2k^2).$ From this, we see that there is an integer $m$ (namely, $2k^2$) where $n^2 = 2m.$ Therefore, $n^2$ is even,

Here, the author is also using exponentiation, another arithmetical operation, and informally—which is not to say unrigorously—proving statement $(1).$ Conditional introduction, existential instantiation and generalisation, etc. are all implicit.

which is what we wanted to show. ■

P.S. That period/colon/comma suffixing the quantifier in $(0)$ potentially introduces ambiguity (though not in $(0)$ itself as it is thoroughly parenthesised): $$∀x\, Px\to Q,$$ due to the precedence convention of logical symbols, definitely means $$(∀x\, Px)\to Q,\tag{A}$$ while in $$∀x. Px\to Q,$$ is the '.' merely superfluous or intended as a delimiter like so $$∀x\, (Px\to Q)\;?\tag{B}$$ $(\text A)$ and $(\text B)$ are logically inequivalent.

ryang
  • 38,879
  • 14
  • 81
  • 179
  • thank you. So am I correct in understanding that the statement (2) in your example is the conclusion? And what we are trying to prove is the fact that this implication is indeed true? So, to contrast this with pure predicate logic, where one assumes the truth of the premises like {A, ∀xAx->Bx, etc}, a math proof is more about proving that an implication is indeed true? As another example, it would be akin to proving that "All men are mortal" (∀x Men(x)->Mortal(x)) as opposed to building a larger argument from such implications? – boinka Mar 01 '23 at 01:15
  • @boinka 1. Yes. $\quad$ 2. To be accurate: the conclusion is a universal statement (this is typical in mathematics), as its main logical operator is ∀ rather than →. $\quad$ 3. No: also because you are stating a nonexistent contrast, since, as I said in blue above, mathematics theorems too are premised —on axioms (definitions, other theorems, etc.), which you can think of as background/tacit assumptions. The answer that I linked to illustrates, for example, that these axioms vary between real analysis and complex analysis. – ryang Mar 01 '23 at 04:20
  • @boinka 4. No! Building on previous arguments is precisely what mathematics does. In my answer, try to imagine how much longer and more tedious the proof would be when formalised. – ryang Mar 01 '23 at 04:20
  • For 2-4. I think I phrased it wrong. I see how it is that the proof relies on previous axioms. But what we're doing here is driving an implication Even(n) -> even(n^2). And to do that we truly on a bunch of tacit knowledge that is not mentioned in the proof – boinka Mar 01 '23 at 12:41
  • I guess what I don't understand is how do the arithmetical operations such as multiplication and exponentiation fit into the context of predicate logic? – boinka Mar 01 '23 at 12:43
  • @boinka "what we're doing here is driving an implication Even(n) -> even(n^2)" The implication being derived is actually statement (1); then, deriving the final result statement (2) is elaborated in the last paragraph here. $\quad$ "tacit knowledge that is not mentioned in the proof" The "tacit knowledge" boils down to mathematical interpretation (e.g., how + works) and definitions and previous theorems, which you do explicitly invoke if they are pivotal; – ryang Mar 01 '23 at 13:34
  • mathematical writing, like a logic textbook, is not a formal language even as it is driven by logic, which you can consider form instead of content (I think I may regret this characterisation, so don't quote me). $\quad$ "how do the arithmetical operations fit into the context of predicate logic?" This and this. Have fun! – ryang Mar 01 '23 at 13:35
  • @boinka Just to be clear: expressing statements formally (for example, using quantifiers in epsilon-delta proofs) is useful in mathematics proofs, and this is still in contrast to a formal (syntactic) proof devoid of natural-language communication. – ryang Mar 02 '23 at 06:37
  • Thank you for the extra color. What do you mean by "expressing statements formally" is not the same as a syntactic proof? I thought expressing something "formally" is using a "formal" system. That is, allowing to manipulate the string syntactically – boinka Mar 02 '23 at 16:58
  • @boinka Expressing "there exists a boy who likes pineapple" formally as ∃b P(b) then manipulating it into ¬∀b ¬P(b) can of course be part of a standard non-formal proof. – ryang Mar 07 '23 at 07:07