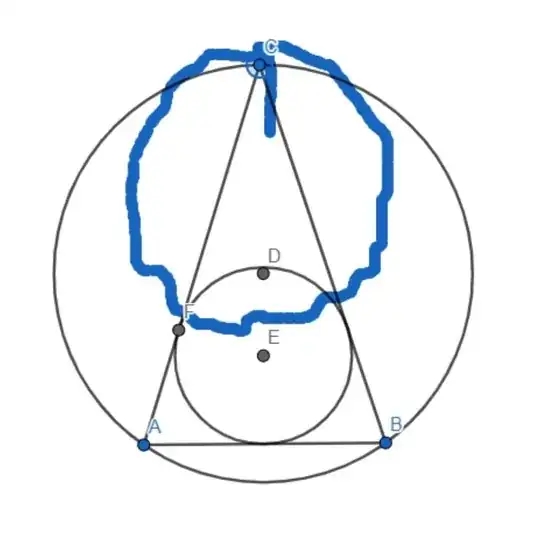
Here is a solution based on ratio $\frac{r}{R}$, where $r$ is the inradius and $R$ the circumradius.
See Geogebra animation here. A static view is available at the bottom of this answer.
$$d^2=R^2-2Rr$$
connecting $r$ and $R$ with $d$ defined as the distance between the incenter $I$ and the circumcenter $O$ of a triangle.
As your inclusion condition is:
$$d \le r,\tag{1}$$
your issue is equivalent to condition :
$$R^2-2Rr \le r^2 \ \iff \ (R-r)^2-r^2 \le r^2$$
Otherwise said, equivalent to :
$$\frac{r}{R} \ge \sqrt{2}-1\tag{2}$$
- Besides, there exists another formula involving ratio $\frac{r}{R}$, which is
$$\frac{r}{R}= \cos(\hat{A})+\cos(\hat{B})+\cos(\hat{C})-1 \tag{3}$$
where $\hat{A},\hat{B},\hat{C}$ are resp. the angles in vertices $A,B,C$ ; see here at paragraph "further conditional identities".
Connecting $(2)$ and $(3)$, the inequality implicitly describing the locus of point $C$ is
$$\cos(\hat{A})+\cos(\hat{B})+\cos(\hat{C}) \ge \sqrt{2}\tag{4}$$
It remains to express (4) in terms of the coordinates $(x,y)$ of $C$.
Intermediate expressions are the sidelengths $a=BC$ and $b=AC$ of triangle $ABC$ given by :
$$\begin{cases}a&=&\sqrt{(x-1)^2+y^2},\\ b&=&\sqrt{x^2+y^2}\end{cases}\tag{5}$$
Relationships (5) are useful in the following expressions of the 3 terms in the LHS of (4) :
$$\begin{cases}\cos(\hat{A})&=&\frac{x}{b}\\
\cos(\hat{B})&=&\frac{(1-x)}{a}\\ \cos(\hat{C})&=&\frac{a^2+b^2-1}{2ab}\end{cases}\tag{6}$$
(the last formula comes from cosine rule : $1=a^2+b^2-2ab \cos \hat{C}$)
It remains to "plug" formulas (5) and (6) into (4) to get the implicit equation of the frontier of the locus. Using a CAS like Geogebra we obtain the following shapes which coincides with the locus given in the answers of Parcly Taxel and Robjohn (with $a=f(x,y)$ and $b=g(x,y)$) ; [the locus itself is the two interior parts of these curves].