1

I would like to generate (i.e. repeatedly compute via a computer) a random periodic function $f(x)$ with period $T$ such that $|f(x)| \leq M$ and the kth Fourier coefficient $|A_k| \leq g(k)$ for a given $g(k)$.

I realize this is kind of open-ended (I'm not giving any information about probability distributions), but is there any way to go about doing this in a way that makes sense?

Here's an example using IPython to plot $$f(\theta)=\cos \theta+\tfrac{1}{2}\cos(3\theta+0.23)+\tfrac{1}{2}\cos(5\theta-0.4)+\tfrac{1}{2}\cos(7\theta+2.09)+\tfrac{1}{2}\cos(9\theta-3)$$ 

th = np.arange(0,1,0.001)
f = lambda th: np.cos(th*2*np.pi)
plt.plot(th,f(th)+0.5*f(3*th+0.23)
  +0.5*f(5*th-0.4)+0.5*f(7*th-2.09)+0.5*f(9*th-3))
plt.ylim([-3, 3])
plt.grid('on')

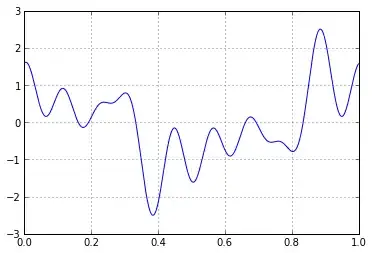
enter image description here

You'll note that $\sum |A_k| = 3$, which implies that $|f(\theta)|<3$, but here the maximum amplitude is around 2.5, because the harmonics never completely add constructively.

So suppose I just want to choose a function $f(\theta)$ such that $|f(\theta)| \leq M = 1.5$ with $|A_1| = 1$, $A_k \leq \frac{1}{2}$ for odd $3 \leq k \leq 21$, and $A_k = 0$ for all other k.

The bound for M is much smaller than the sum of the upper bound of the amplitudes (6.0), and I don't want to turn a random generation problem into a heuristic rejection algorithm.

Willie Wong
  • 73,139
Jason S
  • 3,109
  • What do you mean "generate"? In a computational sense? If $A_k$ is any absolutely summable sequence with $\sum |A_k| < M$, then $f(x)=\sum A_ke^{2\pi ikx/T}$ is a function with period $T$ satisfying $|f(x)|<M$. If you want $f$ to have some regularity, then choose $g(k)$ to decay sufficiently fast... http://math.stackexchange.com/questions/10848/does-rapid-decay-of-fourier-coefficients-imply-smoothness – dls Aug 10 '13 at 20:09
  • yes, a computational sense, let me elaborate; that's too loose of a bound. – Jason S Aug 10 '13 at 20:14
  • If you're going to randomly assign phase shifts, there's no way to get a better bound than what you already said/my previous comment. This is because it's possible to attain the maximum: if you have a cosine series, all phase shifts zero and set $\theta=0$. You're probably better off randomly generating the amplitudes/phase shifts, numerically determining the maximum value of the function and rescaling. But it's still not clear exactly what you're after. – dls Aug 10 '13 at 20:47
  • re: randomly generating + scaling -- that's about what I thought of, but it skews the resulting probability distribution of the coefficients. – Jason S Aug 10 '13 at 21:32
  • From the question, it's not clear to me why this is a problem. How exactly are you using the resulting function? – dls Aug 11 '13 at 22:19

1 Answers1

1

Expecting $|f|\le 1.5$ is much too optimistic. It's right at the edge of the lower bound given by Parseval's identity, and since a trigonometric polynomial of the required form can't possibly look like a constant, its supremum will exceed its root-mean-square by some margin. It's more realistic to shoot for upper bound that's twice the root-mean-square average of $f$.

Taking a cue from Hardy-Littlewood series, I tried to shift $\cos kt$ by $k\ln k$. The results look good: harmonics fight one another all the time, pushing the function up and down. Here is the sum up to $k=11$

k11

and here is the sum up to $k=21$ (I used $1/2$ for all coefficients after the first)

k21

I don't offer a proof of anything, but shifting by $k\ln k$ is "a way that makes sense".

More precisely, I plotted $$\mathrm{Re} \sum A_k\exp( ikt+ik\ln k) = \sum A_k \cos(kt+k\ln k)$$

user90090
  • 1,426
  • 7
  • 6