Compute the integral $\int_{-\infty}^\infty \frac{\sin(x) (1+\cos(x))}{x(2+\cos(x))} dx$

Question

Background

I recently found out about Lobachevsky's integral formula, so I tried to create a problem on my own for which I'd be able to apply this formula. The problem is presented below.

Problem

Compute the integral $\int_{-\infty}^\infty \frac{\sin(x) (1+\cos(x))}{x(2+\cos(x))} dx$

Attempt

If we define $f(x) := \frac{1+\cos(x)}{2+\cos(x)}$, which most definitely is $\pi$ - periodic.

The integral is, using our notation above, on the form

$$I = \int_{-\infty}^\infty \frac{\sin(x)}{x}f(x) dx.$$

The integrand is even, so we might as well compute

$$ I = 2 \int_{0}^\infty \frac{\sin(x)}{x}f(x) dx.$$

We will now have to make use of a theorem.

Lobachevsky's integral formula states that if $f(x)$ is a continous $\pi$ - periodic function then we have that $$ \int_0^\infty \frac{\sin(x)}{x}f(x) dx= \int_0^{\pi/2} f(x) dx.$$

Substituing our $f(x)$ yields us

$$ \int_0^{\pi/2} \frac{1+\cos(x)}{2+\cos(x)} dx = \pi/2 - \int_0^{\pi/2}\frac{1}{2+\cos(x)}dx $$

where

$$I_2 = \int_0^{\pi/2}\frac{1}{2+\cos(x)}dx = \int_0^{\pi/2}\frac{\sec^2(x/2)}{3+\tan^2(x/2)}dx.$$

Letting $ u = \tan(x/2)/\sqrt{3}$, for which $du = \sec^2(x/2)/(2\sqrt{3})dx$, therefore gives us:

$$ I_2 = \int_0^{1/\sqrt{3}}\frac{2\sqrt{3}}{3u^2+3} = \frac{\pi}{3\sqrt{3}}.$$

Finally we can compute $I$ to

$$I = 2\left(\frac{\pi}{2} - \frac{\pi}{3\sqrt{3}}\right) = \frac{\pi(3\sqrt{3}-2)}{3\sqrt{3}}.$$

I've tried calculating this integral in Desmos where it gives me $0$ when I calculate the integrand on the interval $(-\infty, \infty)$, and something negative for $(0,\infty)$. This contradicts my answer.

I also tried typing it into Wolfram, without success. Can anyone confirm the validity of my result?

Answer 1

Another approach:

Using the Fourier series $$1 + 2 \sum_{k=1}^{\infty} (-1)^{n} a^{n}\cos(nx) = \frac{1-a^{2}}{1+2a \cos (x) +a^{2}}, \quad |a| <1, $$ we have

$$ \begin{align} \int_{-\infty}^{\infty} \frac{\sin (x)}{x}\frac{1-a^{2}}{1+2a \cos (x) +a^{2}} \, \mathrm dx &= \int_{-\infty}^{\infty} \frac{\sin (x)}{x}\left(1+2 \sum_{n=1}^{\infty} (-1)^{n} a^{n} \cos(nx) \right) \, \mathrm dx \\ &= \pi + 2 \sum_{n=1}^{\infty} (-1)^{n}a^{n}\int_{-\infty}^{\infty} \frac{\sin (x)}{x} \cos(nx) \, \mathrm dx \\ &= \pi - 2a \int_{-\infty}^{\infty} \frac{\sin (x)}{x} \, \cos (x) \, \mathrm dx + 2 \sum_{n=2}^{\infty} (-1)^{n} a^{n} \int_{-\infty}^{\infty}\frac{\sin (x)}{x} \, \cos(nx) \mathrm dx \\ &= \pi - 2a \left(\frac{\pi}{2} \right)+2\sum_{n=2}^{\infty} (-1)^{n}a^{n}(0) \\ &= \pi \left(1-a \right) . \end{align}$$

Rewriting the integral as

$$\frac{1}{1+a^{2}}\int_{-\infty}^{\infty} \frac{\sin (x)}{x} \frac{1-a^{2}}{1+\frac{2a}{1+a^{2}}\cos(x)} \, \mathrm dx,$$ and letting $a= 2-\sqrt{3}$, we get $$\sqrt{3} \int_{-\infty}^{\infty}\frac{\sin (x)}{x} \frac{1}{2+\cos(x)} \, \mathrm dx = \pi \left(\sqrt{3}-1 \right). $$

Therefore, $$ \begin{align} \int_{-\infty}^{\infty} \frac{\sin (x)}{x} \frac{1+\cos (x)}{2+ \cos (x)} \, \mathrm dx &= \int_{-\infty}^{\infty} \frac{\sin (x)}{x} \, \mathrm dx - \int_{-\infty}^{\infty} \frac{\sin (x)}{x} \frac{1}{2+ \cos (x)} \, \mathrm dx \\ &= \pi - \frac{\pi}{\sqrt{3}} \left(\sqrt{3} - 1 \right) \\ &= \frac{\pi}{\sqrt{3}}. \end{align} $$

The one issue with this approach is justification for switching the order of integration and summation. Fubini's theorem is not satisfied.

---

Fortunately, we can use Sangchul Lee's result from the addendum of this answer to justify the switching.

Answer 2

We start by $$ \int_{-\infty}^\infty \frac{\sin x}{x} \frac{1+\cos x}{2+\cos x}dx {= \sum_{k\in \Bbb Z}\int_{2k\pi}^{2(k+1)\pi} \frac{\sin x}{x} \frac{1+\cos x}{2+\cos x}dx \\= \sum_{k\in \Bbb Z}\int_{0}^{2\pi} \frac{\sin (x+2k\pi)}{x+2k\pi} \frac{1+\cos x}{2+\cos x}dx \\= \int_{0}^{2\pi} \sum_{k\in \Bbb Z}\frac{\sin (x+2k\pi)}{x+2k\pi} \frac{1+\cos x}{2+\cos x}dx \\= \int_{0}^{2\pi} \sum_{k\in \Bbb Z}\frac{\sin (\omega+2k\pi)}{\omega+2k\pi} \frac{1+\cos \omega}{2+\cos \omega}d\omega. } $$ Note that $F(\omega)= \sum_{k\in \Bbb Z}\frac{\sin (\omega+2k\pi)}{\omega+2k\pi}$ and $G(\omega)=\frac{1+\cos \omega}{2+\cos \omega}$ are the Fourier transforms of $x[n]$ and $y[n]$, respectively, where $$ x[n]=\frac{1}{2}\Pi(\frac{n}{2}) \ \ \ ,\ \ \ y[n]=\delta[n]-\frac{1}{\sqrt 3}(-2+\sqrt 3)^{|n|}. $$ Therefore, according to the Parseval's identity we find $$ \int_{0}^{2\pi} \sum_{k\in \Bbb Z}\frac{\sin (\omega+2k\pi)}{\omega+2k\pi} \frac{1+\cos \omega}{2+\cos \omega}d\omega {= \int_{0}^{2\pi} F(\omega) G(\omega)d\omega = 2\pi\sum_{n\in \Bbb Z} x[n]y[-n] \\= 2\pi(x[-1]y[1]+x[0]y[0]+x[1]y[-1]) = \frac{\pi}{\sqrt 3}. } $$

Update

For connecting $F(\omega)$ to $x[n]$, I used the sampling theorem, which is:

Let the Fourier transform of $x(t)$ be $X(f)$. Then, the discrete-time Fourier transform (DTFT) of the sampled signal $\hat x[n]=x(n/F_s)$ is $$ \hat X(f)=F_s\sum_{k\in\Bbb Z} X(F_s(f-k)). $$

I applied the aforementioned theorem to $x(t)=\Pi(t)$ and $F_s=2$.

Answer 3

Utilize the series $$\frac{p\sin x}{1+2p\cos x+p^2}=-\sum_{k=1}^\infty (-p)^{k}\sin kx $$ with $p=2-\sqrt3$ to express
\begin{align} \frac{\sin x}{2+\cos x}= -2\sum_{k=1}^\infty (\sqrt3-2)^k\sin kx \end{align} Then, integrate \begin{align} &\int_{-\infty}^\infty \frac{\sin x}x\frac{1+\cos x}{2+\cos x}dx\\ =& \ 2\int_{-\infty}^\infty \frac{\sin x}xdx- 2\int_{-\infty}^\infty \frac{1}x\frac{\sin x}{2+\cos x}dx\\ =&\ \pi +4\sum_{k=1}^\infty (\sqrt3-2)^k\int_0^\infty \frac{\sin kx}xdx\\ =&\ \pi + 2\pi \sum_{k=1}^\infty (\sqrt3-2)^k= \frac\pi{\sqrt3} \end{align} where the summation is geometric.

Answer 4

There is a generalization of Lobachevsky's integral formula that is applicable.

The formula states that if $f(x)$ is an odd periodic function of period $a$, then $$\int_{0}^{\infty} \frac{f(x)}{x} \, \mathrm dx = \frac{\pi}{a} \int_{0}^{a/2} f(x) \cot \left(\frac{\pi x}{a} \right) \, \mathrm dx \tag{1}$$ if the integral on the left converges.

A proof can be found in the paper The integrals in Gradshteyn and Ryzhik. Part 16: Complete elliptic integrals by Boettner and Moll. It's Lemma 3.1.

The proof says to use the partial fraction expansion of $\tan (z)$. That's clearly a typo. It should be the partial fraction expansion of $\cot (z)$ since $$\sum_{k=0}^{\infty} \left( \frac{1}{x+ka}- \frac{1}{(k+1)a-x} \right) = \frac{1}{x} + \sum_{k=1}^{\infty} \frac{2x}{x^{2}-k^{2}a^{2}} = \frac{\pi}{a} \cot \left(\frac{\pi x}{a} \right).$$

Using $(1)$ and the tangent half-angle substitution, we get $$\begin{align} \int_{-\infty}^{\infty} \frac{\sin(x)}{x} \frac{1+ \cos x}{2+ \cos x} \, \mathrm dx &= 2 \int_{0}^{\infty} \frac{\sin(x)}{x} \frac{1+ \cos x}{2+ \cos x} \, \mathrm dx \\ &= \int_{0}^{\pi} \sin(x) \, \frac{1+ \cos x}{2+ \cos x} \, \cot\left(\frac{x}{2} \right) \, \mathrm dx \\ &= 8 \int_{0}^{\infty} \frac{\mathrm dt}{(t^{2}+1)^{2}(t^{2}+3)} \\&= 4 \int_{0}^{\infty} \frac{\mathrm dt}{(t^{2}+1)^{2}} -2 \int_{0}^{\infty} \frac{\mathrm dt}{t^{2}+1} + 2 \int_{0}^{\infty}\frac{\mathrm dt}{t^{2}+3} \\ &= 4 \left(\frac{\pi}{4} \right) - 2 \left( \frac{\pi}{2} \right) + 2 \left( \frac{\pi}{2\sqrt{3}} \right) \\ &= \frac{\pi}{\sqrt{3}}. \end{align} $$

---

To emphasize what is stated in the paper, if $g(x)$ is an even $\pi$-periodic function, then $g(x) \sin(x)$ is an odd $2 \pi$-periodic function, and $$ \begin{align} \int_{0}^{\infty} \frac{g(x) \sin (x)}{x} \, \mathrm dx &= \frac{1}{2} \int_{0}^{\pi} g(x) \sin(x) \cot \left(\frac{x}{2} \right) \, \mathrm dx \\ &= \frac{1}{2} \int_{0}^{\pi} g(x) \sin(x) \, \frac{1+ \cos(x)}{\sin(x)} \, \mathrm dx \\ &= \frac{1}{2} \int_{0}^{\pi} g(x) \, \mathrm dx + \frac{1}{2} \int_{0}^{\pi} g(x) \cos (x) \, \mathrm dx \\ &= \int_{0}^{\pi/2} g(x) \, \mathrm dx + \frac{1}{2} (0) \\ &= \int_{0}^{\pi/2} g(x) \, \mathrm dx \end{align}$$ which is Lobachevsky's integral formula.

It wasn't immediately clear to me why $$\int_{0}^{\pi} g(x) \cos(x) \, \mathrm dx =0. $$

But since $g(x) \cos(x)$ is an even function, we have $$\int_{0}^{\pi} g(x) \cos(x) \, \mathrm dx = \int_{-\pi}^{0} g(x) \cos (x) \, \mathrm dx. $$

And making the substitution $u = x- \pi$, we have $$\int_{0}^{\pi} g(x) \cos(x) \, \mathrm dx = -\int_{-\pi}^{0} g(u) \cos (u) \, \mathrm du. $$

The only way both equations can be simultaneoulsy true is if $$\int_{0}^{\pi} g(x) \cos(x) \, \mathrm dx=0. $$

Answer 5

$\newcommand{\d}{\,\mathrm{d}}$I can tell you from long personal experience that Desmos is really really really really bad at doing trigonometric integrals over large domains. For example, we all know: $$\int_0^\infty\frac{\sin x}{x}\,\mathrm{d}x=\frac{\pi}{2}$$But:

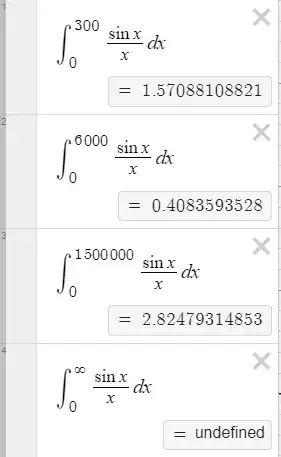
If you play around with the size of the upper bound, Desmos' answer wavers between $0$ and $3$, roughly, and the differences don't at all converge. For reference, $\pi/2\approx1.570796$.

Let's try some others. For example: $$\int_0^\infty\sin(x^2)\d x=\frac{1}{2}\sqrt{\frac{\pi}{2}}$$

Yet:

Which is atrocious.

I could give more examples, but I hope I've made my point: if your integrand features trigonometric quantities that don't really rapidly decay, don't use Desmos, use Wolfram or some other computer.

---

As commented, the period of your $f$ is not $\pi$ but rather $2\pi$. This breaks the formula, so we need another method.

How else can we compute this integral? Complex analysis!

Rewrite the integrand: $$\frac{\sin x}{x}\left(1-\frac{1}{2+\cos x}\right)$$So that our integral is just: $$\pi-\int_{-\infty}^\infty\frac{\sin x}{x}(2+\cos x)^{-1}\d x=\pi-2\alpha\cdot\Im\int_{-\infty}^\infty\frac{1}{\alpha+\beta\cdot e^{-ix}}\cdot\frac{\d x}{x}$$Where: $$\alpha=\frac{\sqrt{3}+1}{2},\,\beta=\frac{\sqrt{3}-1}{2}$$

If we take the contours $-R\to-1/R$ (straight line), $-1/R\to1/R$ (semicircle of radius $1/R$), $1/R\to R$ (straight line) and then $R\to-R$ (semicircle of size $R$) for large $R$ which are uniformly bounded away from the moduli of the poles (see below), $n$ an integer, and limit as $R\to+\infty$, our remaining integral shall equal: $$\Im\left[2\pi i\cdot\sum\operatorname{Res}_{\Im z>0}+\frac{\pi i}{\alpha+\beta}\right]=\frac{\pi}{\alpha+\beta}+2\pi\cdot\Re\sum\operatorname{Res}_{\Im z>0}$$ Since it's not too hard to see that the integrals over the larger semicircles vanish as $R\to\infty$, and the integrals smaller semicircles near zero can be found with the half-residue principle. This would yield a genuine evaluation of the integral of the imaginary part (which converges) and a principal value (of zero) for the non-convergent real part. I here have only focused on the desired imaginary part.

When does our integrand have poles in the upper half plane? If $\alpha+\beta\cdot e^{-i\sigma+\tau}=0$ for some $z=\sigma+i\tau$ then we know $e^{-i\sigma+\tau}=-\frac{\alpha}{\beta}=-2\alpha^2$ which is purely real. Hence $\sigma$ must $\pi n$ for some integer $n$, and then $(-1)^n\cdot e^{\tau}=-2\alpha^2<0$ shows $n$ is necessarily an odd integer. Then $\tau=\ln(2\alpha^2)$ is forced: let's define $\zeta:=\ln(2\alpha^2)$. The poles are precisely $z=\pi(2n+1)+i\zeta$ for integer $n$. The residues are $\frac{1}{z}\cdot\frac{1}{-i\beta e^{-iz}}=\frac{i}{-2\alpha^2\beta}\cdot\frac{1}{\pi(2n+1)+i\zeta}=-2i\beta\cdot\frac{\pi(2n+1)-i\zeta}{\zeta^2+\pi^2(2n+1)^2}$. Thus the integral is: $$\frac{\pi}{\sqrt{3}}-4\pi\beta\zeta\cdot\sum_{n=-\infty}^\infty\frac{1}{\zeta^2+\pi^2(2n+1)^2}$$The other part of the sum, with summands $-2\beta i\cdot\frac{\pi(2n+1)}{\zeta^2+\pi^2(2n+1)}$, I have ignored since the residue sums arise symmetrically, and these summands have (almost) an odd symmetry in $n$ and the sums vanish. This confirms the clear fact that the principal value of the non-convergent real part is zero.

Our final answer should then be: $$\int_{-\infty}^\infty\frac{\sin x}{x}\cdot\frac{1+\cos x}{2+\cos x}\d x=4\pi\zeta\sum_{n=-\infty}^\infty\frac{1}{\zeta^2+\pi^2(2n+1)^2}-\frac{\pi}{\sqrt{3}}=\frac{\pi}{\sqrt{3}}$$

This matches the Wolfram Alpha numerical data. The final series computation was done using well known formulae: $$\forall a,b\in\Bbb R\setminus\{0\},\quad\quad\sum_{n=-\infty}^\infty\frac{1}{a^2+b^2(2n+1)^2}=\frac{\pi}{2ab}\tanh\left(\frac{\pi a}{2b}\right)$$Which can itself be derived from complex analysis. There is a master theorem:

Let $f:\Bbb C\to\hat{\Bbb C}$ be a meromorphic function with a finite set of poles $P$, none of which are integers, such that $\lim_{z\to\infty}zf(z)=0$. Then: $$\lim_{N\to\infty}\sum_{|n|\le N}f(n)=-\pi\sum_{p\in P}\operatorname{Res}_{s=p}(\cot(\pi s)f(s))$$

This can be strengthened a little bit. You need to apply it to the meromorphic map $s\mapsto(a^2+b^2(2s+1)^2)^{-1}$, with poles: $$s=-\frac{1}{2}\pm\frac{a}{2b}i$$