1

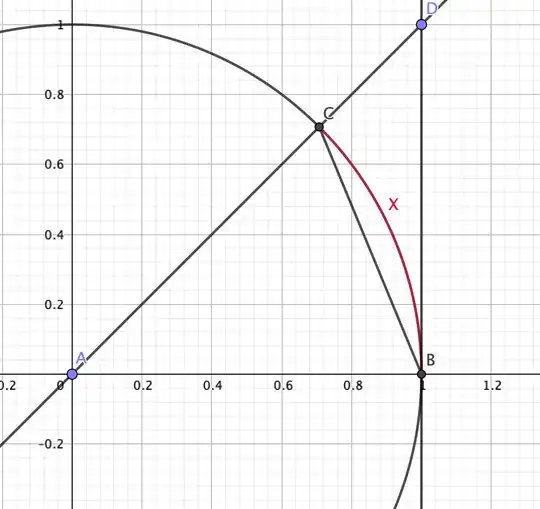
As part of proving that $\frac{\sin{x}}{x}$ tends to $1$, as $x$ tends to zero I am told to consider the following figure and show that $\sin{x}\leq x \leq \tan{x}$ by considering areas.

enter image description here

It is clear to me that $\text{Area}(\triangle ABC)=\frac{\sin{x}}{2}$, $\text{Area(circle section)}=\frac{x}{2}$ and $\text{Area}(\triangle ABD)=\frac{\tan{x}}{2}$. Thus I just need to show the order of these areas.

My thought was describing the areas in terms of sets of points (A naive way of thinking about area, but I haven't learned about integrals and measures yet). For $0<x<\frac{\pi}{2}$ consider:

$H_1=\{(s,t):t\geq 0\}$, $H_2=\left\{(s,t):t\leq\tan{x}\cdot s\right\}$, $H_3=\{(s,t):t\leq \frac{-\sin{x}}{1-\cos{x}}s+\frac{\sin{x}}{1-\cos{x}}\}$, $H_4=\{(s,t):s\leq 1\}$, $C =\{(s,t):s^2 + t^2 \leq 1\}$.

Let $M_1$ be the set of point of $\triangle ABC$, $M_2$ be the set of points in the circlesection and $M_3$ be the set of points in $\triangle ABD$. It is clear that $M_1 = H_1\cap H_2 \cap H_3$, $M_2 = H_1\cap H_2 \cap C$, $M_3 = H_1\cap H_2 \cap H_4$.

The part that I am struggling with is showing $M_1\subseteq M_2$. Since any point $p\in M_1$ must satisfy $p\in H_1 \land p \in H_2$, what I have to show is solely that $s^2 + t^2 \leq 1$ given $0<x<\frac{\pi}{2}$ and assuming $t \geq 0$, $t \leq \tan{x}\cdot s$, $t\leq \frac{-\sin{x}}{1-\cos{x}}s+\frac{\sin{x}}{1-\cos{x}}$.

I have given this a few solid goes by multiplying and squaring inequalities in different ways, but seem rather stuck at the moment. Many thanks for the help in advance.

TShiong
  • 1,257
Frederik Overgaard Nielsen
  • 51
  • 5
  • 6
    I guess you are not supposed to be this formal for this specific question. When you see that one area is contained in another area, I think you may assume that one area is smaller than the other. – student91 Feb 23 '23 at 12:55
  • with an emphasis on see – student91 Feb 23 '23 at 13:31
  • When you talk about "area" you are unavoidably dealing with measures. As mentioned above, the purpose of this exercise is probably not to present a logically rigid proof but rather an intuitive way to understand the inequality. – WhatsUp Feb 23 '23 at 13:43
  • Right -- showing that the areas are related to the function, I think, is the part where you're supposed to show rigor. The areas are inside each other by construction -- you can make a slightly more formal argument because a secant is always inside the circle, and a tangent is always outside – Alex K Feb 23 '23 at 13:46
  • Possibly related to How to prove that $\lim\limits_{x\to0}\frac{\sin x}x=1$?. – robjohn Sep 02 '23 at 11:08

2 Answers2

1

Let $f(x)=\sin x -x\implies f'(x)=\cos x-1 <0~ \forall~ x\in[ 0,\pi/2)$. This implies that $f(x)$ is a decreasing function. Then $f(x)\le f(0)$, hence $\sin x \le x$.

Next, take $g(x)=\tan x-x \implies g'(x)=\sec^2x-1 =\tan^2x>0$. Thins means $g(x)$ is an increasing function $ ~\forall ~ x\in [0,\pi/2)$. Then, $g(x)\ge g(0) \implies \tan x \ge x.$

Z Ahmed
  • 43,235
1

  • In isosceles triangle $ABC$, let $H$ be the foot of the altitude issued from $A$ onto $BC$. We have a right triangle $AHC$. The area of $ABC$ is twice the area of $AHC$ giving $2 \times (\tfrac12 CH \times AH) = \sin(\tfrac12 x) \cos(\tfrac12 x)$ (rotate triangle $AHC$ by angle $-\frac{x}{2}$ for a convincing proof). As a consequence, the area of $ABC$ is equal to $\tfrac12 \sin x$ using the classical trigonometry formula $2 \sin a \cos a= \sin 2a$.

  • The area of circular sector $ABC$ bounded by (red) arc $BC$ is $\tfrac12 x.$ (see here).

  • The area of triangle $ABD$ is $\tfrac12 AB \times BD = \tfrac12 \tan x $.

As a consequence of the successive inclusion of the three sets above :

$$\tfrac12 \sin x < \tfrac12 x < \tfrac12 \tan x.$$

Jean Marie
  • 81,803