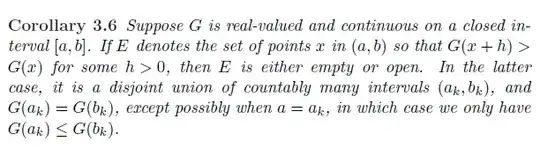I'm struggling to understand the lemma 3.5 and corollary 3.6, but some points make me difficult to fully understand. Before start, let me upload the lemma and corollary. There are 2 questions in total.
Here is the first question about them.
(1) The last sentence of corollary 3.6 says $G(a_k) \le G(b_k)$ when $a = a_k$, but this isn't clear for me, because the previous lemma says $G(a_k) = G(b_k)$ where $E = \cup_k (a_k, b_k)$. The only difference between the lemma and this corollary is the support of the function $G$: $G$ is continuous on all $\mathbb R$ in lemma 3.5, while the $G$ of corollary 3.6 is defined on $[a,b]$. Then, what makes the relationship between $G(a_k)$ and $G(b_k)$ different? I proved the lemma by showing that $G(a_k) < G(b_k)$ doesn't occur due to the fact that $a_k \notin E$, so the fact that inequality $G(a_k) < G(b_k)$ holds in corollary 3.6 makes me confusing.
======================================================
Before asking the second question, let me post the theorem 3.4 and its proof. Although the proof is quite long, it is necessary in this question because I can show you where I'm stuck on.
This is the end of proof of theorem 3.4
(2) The proof says $E_\gamma \subset \cup_{k}(a_k, b_k)$ where $F(b_k) - F(a_k) \ge \gamma(b_k - a_k)$. I'm just assuming this is related to the last sentence of corollary 3.6 ($G(a_k) \le G(b_k)$), but I'm not sure how exactly (mathematically) this leads to the previous inequallity $E_\gamma \subset \cup_{k}(a_k, b_k)$. Also, there exist $G(x) = -F(-x) + rx$, $G(x) = F(x) - Rx$ in the latter part of the proof, as well as their corresponding inequalities $F(b_k) - F(a_k) \le r(b_k - a_k)$ and $F(b_{k,j} - F(a_{k,j}) \ge R(b_{k,j} - a_{k,j})$. I guess this is also associated with the previous definition of $G(x) = F(x) - \gamma x$ , but I'm not sure. I want to clarify how the inequalities $F(b_k) - F(a_k) \le r(b_k - a_k)$ and $F(b_{k,j} - F(a_{k,j}) \ge R(b_{k,j} - a_{k,j})$ are induced from each definition of $G(x)$. (maybe duplicated questions)
Any help would be greatly appreciated. Thank you.