What is the intuitive or geometric explaination of fractional derivatives?

Question

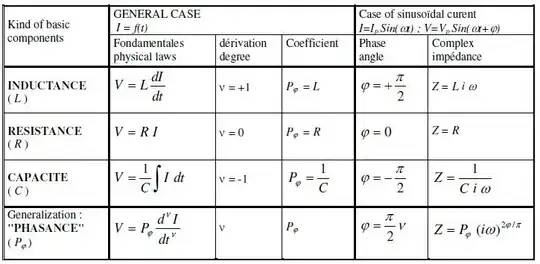
I'm starting to study more advanced solid mechanics, particularly understanding elastomers' stress strain relationships and creep. A common way of describing the variation in the aforementioned relationship as the material is cycled to describe energy loss due to entropy change and this is mathematically described using fractional derivatives.

Is there an intuitive description for a fractional derivative? To use extremely simple calculus examples, by intuitive, I mean the way derivatives are described as rates of change of one variable with respect to another and integrals are described as net change. Or a geometric interpretation such as slopes of lines and areas under curves.

Answer 1

You know that $D_x^2 \sin(ax)=-a^2\sin(x)$; taking two derivatives is like multiplying by the frequency squared. This is an informal way of saying that the derivative is a Fourier multiplier. We can think of the Laplacian operator in Fourier space as $$(-\Delta)f = [|\xi|^2\hat{f}(\xi)]^{\vee}$$ and thus define the operator $D_x^\alpha$ $$D_x^\alpha f = (-\Delta)^{\alpha/2}f = [|\xi|^\alpha\hat{f}(\xi)]^{\vee}$$ which is referred to as the homogeneous derivative. This operator is useful when bounding quantities in well-posedness proofs for certain types of partial differential equations (for example).

What about the inverse to the Laplacian? Integration is a smoothing operator, which can be seen on the frequency side as division. If you take $\alpha<0$ above you get the Riesz potential. You can think of this operator as a spatial convolution. Justification for this way of thinking is provided by the Hardy-Littlewood-Sobolev inequality.

Answer 2

Fractional derivatives are essentially analytic continuation of the concept of the differential operator (or the antiderivative) into a unified differintegral operator, in the same way that the gamma function is the analytic continuation of the factorial function, so grasping for intuitive or geometric explanations isn't exactly easy.

You can think of speed as the first derivative of distance and acceleration as the second derivative of distance, and the 3/2 derivative as somewhere between speed and acceleration, but that's mostly just playing because only differential orders of integers have a local meaning:

https://en.wikipedia.org/wiki/Fractional_calculus#Nature_of_the_fractional_derivative

Fractional Derivative Implications/Meaning?

It's probably better to think of the fractional derivative as a special form of integral rather than a derivative, so the best geometric interpretation I can suggest is its the area under the curve multiplied by the reciprocal gamma function of the order.

Answer 3

Relevant information about the geometric interpretation of fractional derivatives can be found in those papers :

http://www.mathem.pub.ro/dgds/v15/D15-ta.pdf

http://www.scielo.org.mx/pdf/rmf/v60n1/v60n1a6.pdf

http://www.gauge-institute.org/calculus/FractionalCalculus.pdf

http://www.rxiv.org/pdf/1206.0005v1.pdf

Intuitive interpretation in physic, in case of MIXED phenomena which models are some functions, classical derivatives and/or classical antiderivatives of them. This leads to a common behaviour represented by fractional derivatives. A clear example can be shown in electrical impedance analysis : Next Table comes from

http://fr.scribd.com/doc/14686539/The-Fractional-Derivation-La-derivation-fractionnaire

Some models for mixed electrical phenomena are discussed in the paper : http://fr.scribd.com/doc/71923015/The-Phasance-Concept