In $\triangle ABC$ with an internal point $D$, find the measure of $\angle DCA$

Question

As title suggests, the problem is as follows:

We're given a triangle $\triangle ABC$ where $D$ lies inside the triangle. We know that $\angle DBA=10^\circ, \angle DBC=20^\circ, \angle DAB=30^\circ$ and $\angle DAC=50^\circ$. The goal is to find the measure of $\angle DCA=x$

I will share my own solution below as an answer, please let me know if there is anything wrong in it. Furthermore, I'd like to see any other different ways to approach this (such as via trigonometry, analytical geometry, etc) so please share your own approaches as well.

Answer 1

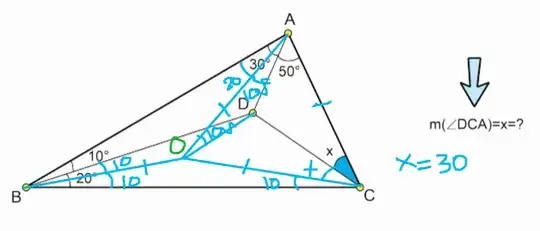
Here is a (completely changed) solution using trigonometry.

Let $I$ be the intersection point of $AC$ and $BD$.

The main observation is that $AIB$ is a right triangle because the sum of angles in $A$ and $B$ is $90°$ ; $BI \perp AD$; as a consequence, $BIC$ is also a right triangle.

Let $BD=a, DI=b, AI=c, IC=d$.

The sine law gives :

$$\begin{cases}\text{in triangle DIA : } \frac{b}{c}&=&\tan(50°)\\ \text{in triangle DIC : }\frac{b}{d}&=&\tan(x)\end{cases} \implies \frac{c}{d}=\frac{\tan(x)}{\tan(50°)}\tag{1}$$

$$\begin{cases}\text{in triangle AIB : } \frac{c}{a+b}&=&\tan(10°)\\ \text{in triangle CIB : }\frac{d}{a+b}&=&\tan(20°)\end{cases} \implies \frac{c}{d}=\frac{\tan(10°)}{\tan(20°)}\tag{2}$$

Equating values in relationships (1) and (2) :

$$\tan(x)=\frac{\tan(10°)\tan(50°)}{\tan(20°)}=\frac{\tan(10°)}{\tan(20°)\tan(40°)}$$ $$\implies x=30°,\tag{3}$$

the last implication being due to a relation which is a close parent of the so-called "Morrie's law" (mentioned at the bottom of this article) saying that :

$$\underbrace{\tan(20°)\tan(40°)\tan(80°)}_{\frac{\tan(20°)\tan(40°)}{\tan(10°)}}=\tan(60°)$$

Answer 2

Here's my approach:

1.) Locate the circumcenter of $\triangle ABC$ and label it $O$. Connect all the vertices of the triangle to the circumcenter. This means that $AO=BO=CO$. Via the inscribed angle theorem, we know that $\angle AOC=2•\angle ABC=60^\circ$. Since $AO=CO$, this implies that $\triangle AOC$ is equilateral, therefore $AO=BO=CO=AC$.

2.) This implies that $\angle OAB=\angle OBA=20^\circ$ and $\angle OCB=\angle OBC=10^\circ$. This also means that $\angle OAD=\angle OBD=10^\circ$. This proves that Quadrilateral $ADOB$ is a cyclic quadrilateral, which means that $\angle AOD=\angle ABD=10^\circ$. This means that $OD=AD$, therefore $\triangle CAD$ and $\triangle COD$ are congruent via the SSS property. This means that $\angle DCA=\angle DCO=x$. $2x=60^\circ$, therefore $x=30^\circ$

Answer 3

A very detailed easy trigonometry approach (not beautiful though) using the law of sines could be as below:

It is very easy to see that $\angle DHC=90^{\circ}.$ Therefore:

$$\sin x^{\circ}=\frac{DH}{DC}=\frac{DH}{AD} \times\frac{AD}{BD} \times\frac{BD}{DC} \\ =\sin 50^{\circ} \times \frac{\sin 10^{\circ}}{\sin 30^{\circ}}\times \frac{\sin (70^{\circ}-x^{\circ})}{\sin 20^{\circ}} =\sin 50^{\circ}\times \frac{\sin (70^{\circ}-x^{\circ})}{\cos 10^{\circ}} \\ \implies \sin x^{\circ}\cos 10^{\circ}=\sin 50^{\circ}\times \sin (70^{\circ}-x^{\circ})\\ \implies \sin x^{\circ}\sin 80^{\circ}=\cos 40^{\circ}\times \sin (70^{\circ}-x^{\circ}) \\ \implies 2\sin x^{\circ}\sin 40^{\circ}=\sin (70^{\circ}-x^{\circ}) =\cos x^{\circ} \cos 20^{\circ}-\sin x^{\circ}\sin 20^{\circ} \\ \implies \frac{\cos x^{\circ}}{\sin x^{\circ}}=\frac{2\sin 40^{\circ}+\sin 20^{\circ}}{\cos 20^{\circ}}=\frac{\sin 40^{\circ}+\cos 10^{\circ}}{\cos 20^{\circ}}=\frac{\sin 40^{\circ}+\sin 80^{\circ}}{\cos 20^{\circ}}=2\sin60^{\circ} \\ \implies x=30^{\circ}.$$

---

To simplify the identities, $\sin a+\sin b= 2 \sin(\frac{a+b}{2})\cos(\frac{a-b}{2})$ was applied.

---