Why is $\langle a,b,c,d\mid abcda^{-1}b^{-1}c^{-1}d^{-1}\rangle\cong \langle a,b,c,d\mid aba^{-1}b^{-1}cdc^{-1}d^{-1}\rangle$?

Question

We have two ways to present a surface of genus 2: (see Identifying the two-hole torus with an octagon)

Now, if one were to calculate the fundamental groups of the above surfaces using van Kampen's theorem, we would get that

$$\langle a,b,c,d\mid abcda^{-1}b^{-1}c^{-1}d^{-1}\rangle\cong \langle a,b,c,d\mid aba^{-1}b^{-1}cdc^{-1}d^{-1}\rangle.$$

While I do understand that this clearly constitutes a proof of the highlighted fact, for a while now, I have been struggling to find a purely algebraic method of finding an isomorphism between the two presentations above. I've tried manipulating the letters of the free groups, as one usually does, to find such an isomorphism to no avail. How may I approach this differently?

Any help at all will be much appreciated.

Answer 1

The following map works: $$ \begin{align*} \phi: a&\mapsto ac^{-1}d^{-1}\\ b&\mapsto dcb\\ c&\mapsto dc^{-1}d^{-1}\\ d&\mapsto dcd^{-1}c^{-1}d^{-1} \end{align*} $$ This map satisfies $\phi(abcda^{-1}b^{-1}c^{-1}d^{-1})=aba^{-1}b^{-1}cdc^{-1}d^{-1}$. Therefore, it defines a homomorphism from one group to the other. Moreover, it is also a free group automorphism, and from this you can use Tietze transformations to show that the map is infact an isomorphism (other ways of proving this are also available!).

More generally:

Lemma. Suppose $\phi:F(\mathbf{x})\to F(\mathbf{y})$ is an isomorphism of free groups. Then the one-relator presentations $\langle \mathbf{x}\mid R\rangle$ and $\langle \mathbf{y}\mid \phi(R)\rangle$, and also $\langle \mathbf{y}\mid \phi(R)^{-1}\rangle$, define isomorphic groups.

The map isn't magic. I found the above map with a bit of guesswork/intuition, but crucially I could have found it algorithmically (and I think someone has implemented the algorithm, I just can't remember who, or find their implementation!). The algorithm in question is an algorithm of Whitehead, which is really well understood.

Crucially, if the two groups were isomorphic then a map of this form must exist - that is, the above lemma can be reversed. This is surprising, and not always true. Indeed, it was the subject of an old conjecture of Magnus from the 1960s:

Conjecture (false). Two one-relator presentations $\langle \mathbf{x}\mid R\rangle$ and $\langle \mathbf{y}\mid S\rangle$ define isomorphic groups if and only if there is an isomorphism of free groups $\phi:F(\mathbf{x})\to F(\mathbf{y})$ with $\phi(R)=S$ or $\phi(R)=S^{-1}$.

This would have reduced the isomorphism problem for one-relator groups to Whitehead's algorithm. Sadly the conjecture is false, but is true for some classes of one-relator groups. Lets say the groups are "naturally isomorphic" if the above isomorphism condition holds. Then:

1. In the 1970s, Pride proved that if $|\mathbf{x}|=2$ and there exists a word $T\in F(\mathbf{x})$ and an exponent $n>1$ such that $R=T^n$ in $F(\mathbf{x})$ (so $\langle \mathbf{x}\mid R\rangle$ is a two-generator, one-relator group with torsion), then $\langle \mathbf{x}\mid R\rangle\cong\langle \mathbf{y}\mid S\rangle$ if and only if they are naturally isomorphic.
2. In the early 2000s, Kapovich and Schupp proved that the condition almost always holds, or more formally that there is a generic class $\mathcal{C}$ of one-relator presentations such that if $\langle\mathbf{x}\mid R\rangle\in\mathcal{C}$, then $\langle \mathbf{x}\mid R\rangle\cong\langle \mathbf{y}\mid S\rangle$ if and only if they are naturally isomorphic.
3. More relevant to the case here: if $\langle \mathbf{x}\mid R\rangle$ defines a surface group, then $\langle \mathbf{x}\mid R\rangle\cong\langle \mathbf{y}\mid S\rangle$ if and only if they are naturally isomorphic. This follows from an unpublished result of Louder from 2010 (arXiv:1009.0454), although his result is more general and so I suspect a older, published result would suffice.

To summarise: all you need to do is find an automorphism $\phi$ of $F(a, b, c, d)$ such that $$\begin{align*}\phi(abcda^{-1}b^{-1}c^{-1}d^{-1})&=aba^{-1}b^{-1}cdc^{-1}d^{-1}\\ \text{or}\qquad\phi(abcda^{-1}b^{-1}c^{-1}d^{-1})&=(aba^{-1}b^{-1}cdc^{-1}d^{-1})^{-1}. \end{align*}$$ This is decidable by an algorithm of Whitehead, or by a bit of intuition and some guesswork... The map $\phi$ at the start satisfies this, so we're done.

Answer 2

I will mark the inverse of an element in a group by using a bar. The present solution is supported by the topological insight, we have two isomorphic spaces, $X$, $Y$, so at the level of the fundamental groups we also functorially get an isomorphism between $G=\pi_1(X)$ and $H=\pi_1(Y)$. The groups $G$, $H$ come as groups with generators and presentations, so it remains to translate the structure at this level. Giving a map leads to a quick solution, since it is easy to check algebraically that the one presentation of the one group goes to a presentation equivalent to the one of the other group.

However, a "fair solution" should make this translation explicit. It is what i am trying below. It is the reason for a potpourri of drawings, hoping that the idea of identifying the constructions of the two spaces, and of the paths on them becomes clear. Yes, completely forgetting about the topological origin, we are more or less quickly done with an algebraic search, but since the question comes explicitly with this origin, such a solution may be also of interest. The reader in hurry may skip to the third drawing to see the connection at topological level, get the algebraic translation, the check for it doing (almost) the job.

---

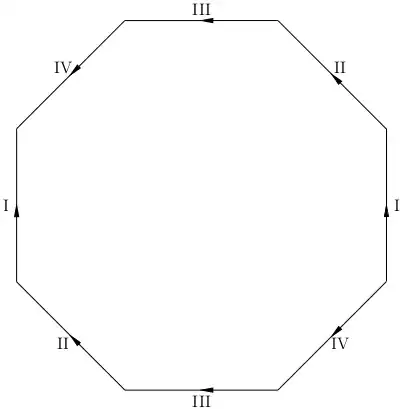
The question asks for a (purely algebraic) isomorphism between the groups: $$ \begin{aligned} G &= \langle\ A,B,C,D\quad \mid\quad ABCD\; \bar A \bar B\bar C\bar D\ \rangle \ , \\ H&= \langle\ a,\ b,\ c,\ d\quad \mid\quad \underbrace{ab\;\bar a\bar b}_{[a,b]}\cdot \underbrace{cd\;\bar c\bar d}_{[c,d]}\ \rangle\ . \end{aligned} $$ Here is a first impression on the construction of $G$ from the octogon with sides, in this order, (identified with "paths") $A,B,C,D;\bar A,\bar B,\bar C,\bar D$. (And also a first note, the composition used while writing the presentation item $ABCD\; \bar A \bar B\bar C\bar D$ feels opposed to the composition of paths. With this in mind, relations below may look also opposite, let us fix this convention, that better suits the group operation in $G$.)

First picture:

This first picture shows roughly the strategy of glueing the sides of the starting octogon, as depicted in $(1)$ above. Denote the resulted space by $X$. We stretch both opposite $A$-sides, and form a cylinder after glueing them. Before doing so, it is convenient to also place the two $C$-side close to each other, they are coming next in the glueing process. So after closing the $A$-slit, then the $C$-slit, we have the surface of a torus, with a square cut, the opposite sides of the square still to be glued. This can be done, and some undetailed doodle shows how the second hole comes into play. We expect this, but the question is now how do the paths $A,B,C,D$, which are now closed, live in the picture.

---

In a following second picture we have some instances of the spaces to be compared. The space $X$ was already introduced above, is on the left side, the space $Y$ is the rather standard way to construct (in the particular case $g=2$) a surface of genus $g$.

The question is now how to realize $A,B,C,D$ from the left drawing inside the second one. Since the relation $ABCD=DCBA$ holds in $\pi_1(X)$, just optically transposing it in the second picture would lead to also a relation in $\pi_1(Y)$. This relation must be a follow-up of $[a,b]\;[c,d]=1$, so we get a solution for our problem. To compare accurately, here is a further drawing.

---

Third drawing:

This third drawing repeats the steps from the first picture, but the focus is on the correct placement of the paths $A$ and $C$. For clarity, only $A$ was finally drawn. Some words on the above. We start as in the first picture with the octogon $(1)$ with opposite sides identified, this time also showing how the vertices move in the pasting process, so stretch the $A$ sides first, get them closer, close their slit, then the same with the $C$-sides, we have a torus with some square removed, opposite sides of the square still to be identified, and we redraw $(3)$ by making more room for this square with vertices $16$, $47$, $25$, $38$ on the upper surface of the torus. In position $(4)$ we want to identify first the $D$-sides. For this process take some more material from the torus below the $D$ side from $16$ to $38$, and push $D$ somehow "parallely" to itself to get it closer to the position between the oder $D$ side between $47$ and $25$ in the picture. Do not overlap the rubber surfach, instead push the corner $16$ inside the square hole towards $47$, same game for $38$ towards $25$, so that finally the $B$-sides become circle paths in position $(5)$.

In the obtained position $(5)$ we have two boundaries, two holes in the surface of the torus. Collect some more material from the surface of the torus, and let the circular holes slightly grow on some small hills. Now let these hills grow higher in the ambient space, we want them to get closer at some point and glue the two closed $B$-paths with each other. After all, we reach position $(6)$.

This position is now easily compared with the standard picture $(7)$ for the other octogon with sides identified w.r.t. the glueing scheme $[a,b]\;[c,d]=1$. In $(7)$, the genus two surface has two parts, the left one whith paths $a,b$, and the right one with paths $c,d$ as drawn. We already imagine them on the surface in $(6)$.

How does $A$ translate in terms of $a,b,c,d$? First of all, $A$ takes a trip around the left donut, as $b$ does. So $A=bx$. What is the remained path $x$ doing? It goes behind the first/left, behind the second/right hill, climbs this second/right hill on the hidden side, then closes the contour. Imagine it now doing the same in a more slow way, and let it make this trip after going behind the first hill by coming out first between the hills, closing the path, which is a $d$-path (after moving it in the "second ring"), and the remained trip is equivalent to a $c$-trip.

This gives the translation of $A$ as $A=b\cdot dc$.

Do now the same with $C$. By design, $C$ comes down on the second hill first, using the front wall. This is half of $\bar c$, so close the $\bar c$ trip by force, and after doing so, the new trip of $C$ starts from the same point, going down on the first hill on its front side, as $A$ did some minutes ago. But now, the ant on the $C$ path prefers to follow the $a$ circuit, and after all the path is closed with a $d$ path.

This gives the translation of $C$ as $C=\bar c\cdot a\cdot d$.

The translations of $B,D$ are easy, they are $\bar d$ and $c$.

---

So we have the following Ansatz for a map $\varphi$ from $G$ to a quotient group of $K:=\langle a,b,c,d\rangle$, $$ \begin{aligned} A&\to bdc\ ,\\ B&\to \bar d\ ,\\ C&\to \bar cad\ ,\\ D&\to c\ . \end{aligned} $$ Then: $$ \begin{aligned} ABCD\ \bar A\bar B\bar C\bar D & \to bdc\cdot\bar d\cdot \bar cad\color{red}{\cdot c\cdot \bar c}\bar d\bar b\cdot d\cdot \bar d\bar a \color{red}{c\cdot \bar c} \\ &= bdc\cdot\bar d\cdot \bar ca\cdot\color{blue}{d\bar d}\bar b\cdot \color{blue}{d\cdot \bar d}\bar a \\ &= bdc\cdot\bar d\cdot \bar ca\bar b\cdot \bar a \\ &= b\ [d,c]\;[a,\bar b]\ \bar b\ . \end{aligned} $$ The map $\varphi$ thus brings $ABCD\ \bar A\bar B\bar C\bar D$ into "a version" of $[a,b]\; [c,d]$, more exactly, it is a conjugate of $[d,c]\;[a,\bar b]$. So by construction, we obtain first a map from $G$ to $K$ modulo $[d,c]\;[a,\bar b]$ (following the topological insight), and can finish the algebraic problem by further composing with the appropriate map: $$ \left\langle \ A,B,C,D\ \Big|\ ABCD\ \bar A\bar B\bar C\bar D\ \right\rangle \overset\varphi\longrightarrow \left\langle \ a,b,c,d\ \Big|\ [d,c]\;[a,\bar b]\ \right\rangle \longrightarrow \left\langle \ a,b,c,d\ \Big|\ [a,b]\;[c,d]\ \right\rangle \ . $$