Counterintuitive instances of intransitivity

Question

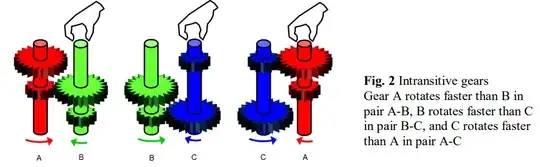
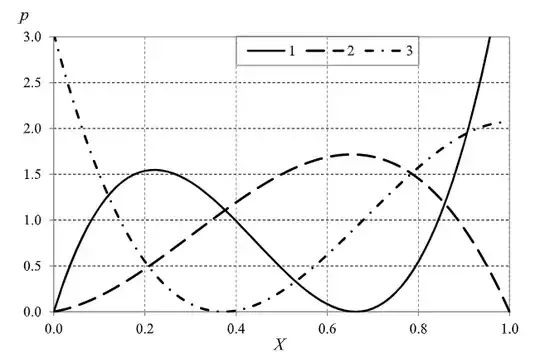
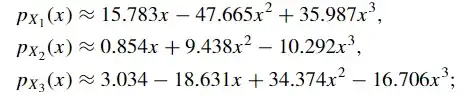Recently, I read a fascinating article by E. Klarreich on intransitive dice. Among other things, the authors give an example of a triplet of dice $A$, $B$, and $C$ such that the probabilities of $A$ beating $B$, $B$ beating $C$, and $C$ beating $A$ are all higher than $1/2$.

The particular example they gave consisted of the three six-faced dice with the following amount of values on each side, all adding up to $21$: $A = (3,3,3,3,5)$, $B =(2,2,2,5,5,5)$, and $C = (1,4,4,4,4,4) $. Now, $A$ beats $B$ on $58\%$ of rolls, $B$ beats $C$ on $58\%$ of rolls, and $C$ beats $A$ on $69\%$ of rolls. Therefore, the transitivity property for this particular triple of dice does not hold: non of them is stronger than the others. According to analytic number theorist B. Conrey (who has co-authored a notable paper on the subject), “It’s not intuitive at all that [intransitive dice] should even exist.”

Another example of intransitivity comes about when considering human preferences for three or more different options to choose from. This sometimes happens, for instance, during political elections. More information on this phenomenon is provided in e.g. the following paper by A. Y. Klimenko.

Though I think the second example is interesting as well, I suppose it has more to do with cognitive and political theory than with formal mathematics. I am mostly curious about counterintuitive examples of intransitivity the first type, which pertain to mathematics itself.

Question: what other counterintuitive instances of intransitivity have been discovered in the field of mathematics?

Answer 1

A simple one that I like is correlation: If $X$ and $Y$ are positively correlated and $Y$ and $Z$ are positively correlated, one might intuit that $X$ and $Z$ are positively correlated. Of course, this is not the case, and they might even be negatively correlated.

For an example, take $A, B, C$ independent standard Gaussians and define $$ X = A + B, \quad Y = B + C, \quad Z = C - A $$ so that \begin{align*} \mathrm{corr}(X, Y) &= \mathrm{corr}(A+B, B+C) = 1/2, \\ \mathrm{corr}(Y, Z) &= \mathrm{corr}(B+C, C-A) = 1/2, \\ \mathrm{corr}(Z, X) &= \mathrm{corr}(C-A, A+B) = -1/2. \end{align*}

Answer 2

Penney's Game, https://en.wikipedia.org/wiki/Penney%27s_game

When repeatedly flipping a fair coin, THH comes up before HHT by a margin of three to one. HHT comes up before HTT by a margin of two to one. HTT comes up before TTH by a margin of three to one, and TTH comes up before THH by a margin of two to one.

Answer 3

Here are some more examples:

1. Chess. Certain combinations of pieces and positions of chess are intransitive. See for instance this paper by Poddiakov. Here is an example of such an intransitive set of positions:

2. Gears. The intransitivity of the rotation speed of certain constellations of gears is described on p. 5 of the following article. Here is an example:

3. The aforementioned article describes many more instances of intransitivity, including intransitive levers, pulleys, wheels, axles, wedges, and ramps. Below one finds an instance of intransitive double levers:

4. One could also interpret the intransitive dice as discrete variables, and generalize them to the continuous case. Gorbunova and Lebedev describe continuous RVs with polynomial densities in this article. The define $$P_{X_{1} X_{2} X_{3}} := \min[ P(X_{1} < X_{2}), P(X_{2} < X_{3}), P(X_{3} < X_{1}) ] > \frac{1}{2} $$ and obtain a lower bound for the maximum of this value when $X_{1}, X_{2},$ and $X_{3}$ have polynomial densities, where the polynomials have degree three and four. For degree three, this is what the optimal collection of polynomials looks like (approximately):

                                  

Here's what these polynomials look like graphically:

   

For some reason, I can't center the above image horizontally.