0

Background: $Y$ turns out to be projective space but I'm trying to prove this and have not proven it yet (i.e., $Y$ is homeomorphic to the space $X$ obtained by identifying antipodal points on the unit $n-$ sphere.)

One of the steps in proving the homeomorphism is to prove that $Y$ is Hausdorff. I am having difficulty in a step in showing the Hausdorffness of Y. I'm trying to use this solution https://math.stackexchange.com/a/241786/266435 in this case.

Let $p_2: \mathbb R^{n+1}-\{0\}\to Y: x\to [x]$ be the quotient map.

Suppose that $[x], [y]\in Y, [x]\ne [y], [l]$ denotes equivalence class of $l$. It follows that $p(x)=[x], p(y)=[y]$. Since $[x]\ne [y]$, it follows that $x\ne my$ for any $m\in \mathbb R-\{0\}$. (i.e., $x$ and $y$ cannot lies on the same line through the 'removed' origin.) $\mathbb R^{n+1}-\{0\}$ is Hausdorff so there exist $U, V$ disjoint open in $\mathbb R^{n+1}-\{0\}$ such that $x\in U, y\in V$.

Now, the following two things are to be shown:

  1. $p(U), p(V)$ are open.
  2. $p(U)\cap p(V)=\emptyset$

I have tried to show that 2) is true as follows: Suppose on the contrary that $p(U)\cap p(V)\ne\emptyset$. There exists $t\in p(U)\cap p(V)$. There exist $u\in U, v\in V$ such that $t=p(u)=p(v)\implies u=mv$ for some non zero real no. $m.\implies u,v$ lie on the same straight line through the origin. This contradicts the fact that $U, V$ are disjoint and that $U,V$ is 'centered' at different lines. But in view of red line in picture no. 2) in the picture below, this seems wrong. 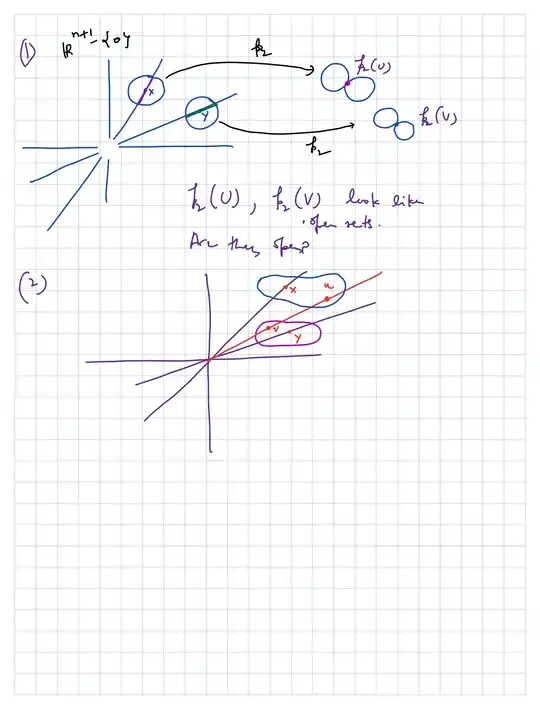enter image description here

About $(1)$, I tried to use the definition of quotient maps: $p_2(U)$ is open iff $p_2^{-1}(p_2(U))$ is open. But since $p_2^{-1}(p_2(U))\ne U$, I'm not sure how to do this either.

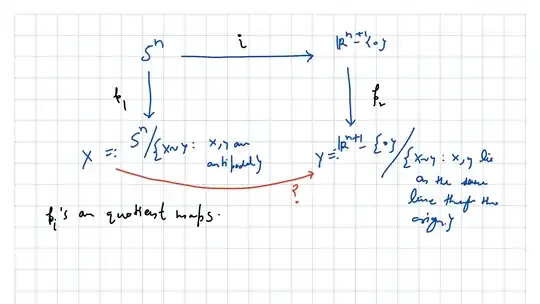
I tried to show the homeomorphism using the following picture: enter image description here

Here, if I show that $Y$ is Hausdorff, then the induced map $p_2\circ i: S^n\to Y$ due to being onto continuous from compact $S^n$ to Hausdorff $Y$ will turn out to be a quotient map. This quotient map partitions $S^n$ into equivalence classes of antipodal points, so by the property of quotient maps, it follows that $X$ is homeomorphic to $Y$. But here the problem is in proving that $Y$ is Hausdorff, and this is what led me to ask this question.

Please advise. Thanks a lot.

Martin Sleziak
  • 53,687
Koro
  • 11,402
  • I think that 2) can be taken care of by choosing $U$ and $V$ very small so that $u$ and $v$ can't be joined by a straight line through the origin. But I still have no idea about how to show 1). – Koro Jan 28 '23 at 06:40
  • Can't you just norm it down to the n-sphere and then use that this space is hausdorff? – justabit Jan 28 '23 at 06:41
  • 1
    @MarianoSuárez-Álvarez: Thanks for the comment. I understand that the inclusion you suggest is compatible with the equivalence as you mention. I'm afraid I don't understand completely the comment after that. For the other direction, one map is $x\mapsto x/|x|$ but I don't understand why it is required and what it will achive. – Koro Jan 28 '23 at 06:48
  • @justabit: Thanks for the comment. What is 'it'? Do you mean $Y$? I'm not sure then because I don't understand how to do operations on $Y$ (here line through origin is being squeezed to a point) so I don't know how to take that into account while taking norm. – Koro Jan 28 '23 at 06:50
  • @MarianoSuárez-Álvarez: I tried to do something similar the other day but not exactly what you suggested. I have included that detail in my post now. Now, coming to finding two mutually inverse homeomorphisms as you suggest: Suppose that I do find it, then I don't understand how it shows the desired homeomorphism? – Koro Jan 28 '23 at 07:05
  • As per the suggestion above: let $in:S^n\to R^{n+1}-{0}:in(x)=x$ and $g:R^{n+1}-{0}\to S^n: g(x)=x/{|x|}$. Here $g\circ(in)=g|_{S_n}$ and not an identity. If it were identify, then it would follow that $g$ is a quotient map. But I don't understand how it helps answer my question. – Koro Jan 28 '23 at 07:22
  • There is an error in my last comment, the correction is as follows: indeed $go(in)$ is an identity on $S^n$ so $g$ is a quotient map. But it implies (using properties of quotient maps) something that is not true: X is homeomorphic to $S^n$. – Koro Jan 28 '23 at 07:25
  • Sorry this is on mobile and @MarianoSuárez-Álvarez formulated it better. I think you can prove your question by showing you can identify Y with the upper half of the n-sphere or at least if a,b in the n-sphere are different, then [a] and [b] are different. Then the disjoint open sets of [a] and [b] follow from $\mathbb{R}^n$. – justabit Jan 28 '23 at 08:12
  • @justabit: I'm still new to this subject and I'm afraid I don't understand your comment. How do I show that Y is Hausdorff? Also I don't understand why the comment about inverse homeomorphism answers my question. I think that existence of such a thing will make X homomorphic to $S^n$, which I think is not correct. – Koro Jan 28 '23 at 08:45

2 Answers2

1

$\mathbb R^{n+1}-\{0\}$ is Hausdorff so there exist $U, V$ disjoint open in $\mathbb R^{n+1}-\{0\}$ such that $x\in U, y\in V$.

This is correct, but it does not help you because you cannot expect that $p(U) \cap p(V) = \emptyset$. Your picture (2) gives a counterexample. By the way, one can show that $p$ is an open map, but this is somewhat tedious and above all unnecessary.

Anyway, you cannot take arbitrary open neighborhoods of $x$ and $y$, but have to make a careful choice.

Your observation that we can identify $Y$ with $S^n/{\sim}$, where $\sim$ identifies antipodal points, is a much better approach. Now look at Brian M. Scott's answer to How can I prove formally that the projective plane is a Hausdorff space? to see how to choose $U, V \subset S^n$.

Here are two questions which may be helpful:

Paul Frost
  • 76,394
  • 12
  • 43
  • 125
  • Thanks for the answer. Unfortunately, I still don't understand the answer to my question (why is $Y$ Hausdorff?). I'll explain: a) I think that the issue in picture titled 1) can be resolved by taking U and V very small. The intuition tells that doing so will ensure that no point in U can be joined to a point of V via a straight line through the origin. b) The linked answer: I am comfortable with the answer but it shows Hausdorffness of $S^n$/~, which is denoted by space X in my post. But I want to show it for $Y$ and as I mentioned in the post, I have not yet shown X and Y to be homeomorphic. – Koro Jan 28 '23 at 18:13
  • But I think that you suggest the following in your answer (Is my understanding correct that you suggest the following): Instead of taking the inclusion map i, I take the map $g:R^{n+1}-{0}\to S^n: x\mapsto \frac x{|x|}$. So in the new diagram, the second picture (the one towards the end of the post): $S^n$ and $X$ appear on the right; $R^{n+1}-{0}$ and X on left, $p_1,p_2$ remain as it is, whereas $i$ is replaced by $g$. Now using the linked answer, X is Hausdorff. And the map $p_1\circ g$ is onto continuous. And this is the point where I get stuck. (Contd.) – Koro Jan 28 '23 at 18:20
  • This is because in the earlier case (the case in post), we have $p_2\circ i:S^n\to Y$, which will be onto continuous from a compact set S^n to a Hausdorff space Y (if Y has been proven to be Hausdorff), and there is a theorem that guarantees that in such a case, $p_2\circ i$ must be a quotient map. So I consider the 'triangle' $S^n X Y$ and conclude that the map induced by $p_2\circ i$ from X to Y is a homeomorphism. But in the case in my last comment, I have $p_1\circ g$ from $R^{n+1}-{0}$ to X, and since $R^{n+1}-{0}$ is not compact, (Contd.) – Koro Jan 28 '23 at 18:25
  • I don't understand how to conclude $p_1\circ g$ to be a quotient map. – Koro Jan 28 '23 at 18:28
  • Thanks a lot :-). In your linked answer, the part showing that $U$ and $V$ are disjoint open with the property $\pi^{-1}(\pi(W))=W$, where W=U or V clears much of my confusion. We get a 'double cone' with its apex removed and indeed it is open. So my question has been answered. Thanks a lot. – Koro Jan 28 '23 at 19:18
0

Ok I try to sketch out a proof for why Y is hausdorff. This is not complete but I hope it will bring you forward. Notationwise, let $x = (x_1,...,x_{n+1}) \in \mathbb{R}^{n+1}$ and $[x]$ the equivalence class of $x$ in $Y$.

  1. You can identify $Y$ with the upper Hemisphere $A$ of the n-Sphere $S^n$, where $x_{n+1} > 0$ be careful at the border $x_{n+1} = 0$, I'm not going to write the details out.
  2. if $a \neq b \in A$ then there is a $n$-dimensional hyperplane $M$ defined by all points that are equally far away from $a$ and $b$. Note that $0$ is part of $M$ while $a$ and $b$ are not. Also it is possible to show, that if $x \in M$, then the straight line through $x$ and $0$ is also in $M$.
  3. Since $M$ is closed, there is a point $m \in M$ which is closest to $a$ which is also closest to $b$. So let $\epsilon$ be the distance of $m$ and $a$ which is also the distance between $m$ and $b$. Now define the $\epsilon$-Ball $B_\epsilon(a)$ of radius $\epsilon$ around $a$ as well as $B_\epsilon(b)$. Since $$ B_\epsilon(a) \cap B_\epsilon(b) = \emptyset $$ the points $[a],[b] \in Y$ are also seperated by $[B_\epsilon(a)]$ and $[B_\epsilon(a)]$ where for a set $U$ $$[U]:= \{[x] \ | x \in U \}$$.

This is just a rough sketch but I hope it will help you out.

justabit
  • 705