0

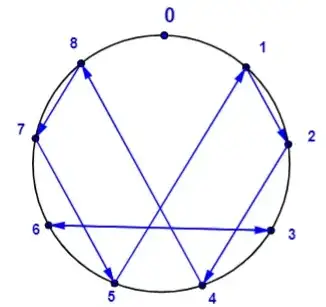
So I was aimlessly scrolling on facebook and ran into a questionable post preaching the spiritual significance of the number 9. Ignoring all the philosophy and spirituality the poster basically notices the following diagram and property and claims that this is unique to the number 9 / at the least the number 9 is a very small number with this property.

So we begin by consider the power of 2s mod 9. That is

$$ 1, 2, 4, 8, 16, 32, 64 ... \mod 9$$

which by fermat's little theorem gives the repeating sequence

$$1, 2, 4, 8, 7, 5, 1, 2, 4, 8, 7, 5 .... $$

Now if you draw this sequence onto a 9-element clock (in black below), by painting a line in order of 1,2,4,8,7,5 (in violet below) and then back to 1 you get the following image:

image of circular clock with 9 hours and with 12-o clock labelled 0 and line passing from 1 -> 2 -> 4 -> 8 -> 7 -> 5 -> 1

Unfortunately I didn't draw my clock and lines correctly to scale BUT if I had it would certainly be symmetric about the center line.

enter image description here

So there are a couple of interesting questions you can ask about this diagram, I'm only interested in (1) for the purposes of this post but I'll include the others if they stimulate some ideas.

  1. Which pairs if numbers $(u,v)$ have the property that $u^n \mod v$ when traced on a v-hour clock like above end up creating an image which is symmetric about the central vertical line. I was able to notice trivially that $(0,2)$ and $(1,2)$ have this property and clearly $(2,9)$ has this property so I'm tempted to ask is $(a,b)$ where $a = 0$ or $(a,b)=1$ enough to guarantee this? Are there exotic examples which don't fall into that category?

Other thoughts:

  1. (Group Angle) Can an exponential sequence and clock pair $(u,v)$ ever make an image which has lines of symmetry that are NOT the center line?

a. In general if we replace the clock with a geometric representation of some arbitrary group and replace the exponential sequence with the sequence $g^n$ for some group element then what are all the possible lines of symmetry we can find via ray-tracing exponential sequences for a particular group

Jean Marie
  • 81,803
Sidharth Ghoshal
  • 16,771
  • 2
    Damn bruh this is some mathematically knowledged crackpot if they use fermats theorem to explain this – tryst with freedom Jan 26 '23 at 21:30
  • 1
    lmao they didn't know about fermats little theorem, but I mentioned on fb that was the underlying cause for this. I still have no good explanation for it being symmetric about the center line so that's why im here asking this. The post is from Jain108Academy on fb and the original image is from Tuzlay Art – Sidharth Ghoshal Jan 26 '23 at 21:31
  • 6
    The symmetry just comes from the fact that it gets to $-1$ mod $v$ then repeats another cycle, but reflected by the $-1$ before getting back to $1$. So it has this symmetry whenever $-1$ is in the sequence. – Zoe Allen Jan 26 '23 at 21:32
  • That was beautifully done! Post it as an answer so I can accept – Sidharth Ghoshal Jan 26 '23 at 21:35
  • @ZoeAllen That blows my mind a bit. This should be true any time $2$ is a primitive root... do we get threefold symmetry when $3$ is a primitive root? Have to test this... – Eric Snyder Jan 27 '23 at 02:56
  • @Tryst with Freedom Please refrain from using slang terms like "damn bruh", not because they are slang but because people like me who haven't english as their mother language don't understand their meaning, and worst than that, aren't able to detect what they "understate", whether they are encouraging, ironic, etc. which is often troublesome. – Jean Marie Jan 27 '23 at 05:22
  • See the nice Geogebra animations here. Take for fun : modulo =50. Pretty envelope, isn't it ? See about this envelope issue the first example in a question of mine here. – Jean Marie Jan 27 '23 at 05:32
  • 1
    I have taken the liberty to include into your question a graphical representation issued from the Geogebra animation I have cited. Feel free to erase it. – Jean Marie Jan 27 '23 at 08:52
  • I think Mathologer (on YouTube) posted something about these patterns within the last year or two, but don't have to search right now. But see this post: https://math.stackexchange.com/questions/2988910/graphical-multiplication-tables-for-mathbbz-p-mathbbz-and-mathbbz – Paul Sinclair Jan 27 '23 at 18:43

0 Answers0