0

The goal would have been for the smallest positive solution of $y\cot(y)=x$ using a Dirac $\delta(x)$ Fourier series and the Bateman function:

$$y\cot(y)=x\mathop\implies^?\frac1{\sec^2(y)-x}=\int_0^\frac\pi2\delta(\tan(t)-xt)dt$$

However, when testing $x=2$, or any other values:

$$\tan(y)-2y=0\implies\frac1{\sec^2(y)-2}\mathop=^\text{should}\int_0^\frac\pi2\delta(\tan(t)-2t)dt=0.2255\dots$$

according to Dirac delta function of a function and Wolfram Alpha. Approximating by a $\delta(x)$Fourier series:

$$\frac1{\sec^2(y)-2}\mathop=^?\lim_{N\to\infty}\frac1{2\pi}\int_0^\frac\pi2\sum_{n=-N}^N e^{i n(\tan(t)-2t)}dt\approx0.72$$

with Wolfram Alpha giving $0.72$ after $N=150$ terms. If this were the true value of the integral, then $\frac1{\sec^2(y)-2}=0.72\implies y\approx 0.99$ when really $\tan(y)-2y=0\implies y=1.16556\dots$

We get about the same integral with a $\delta(x)$ limit approximation. If not for this issue, we would have a solution like the Kepler equation Bessel series for $y\cot(y)=x$.

Side information

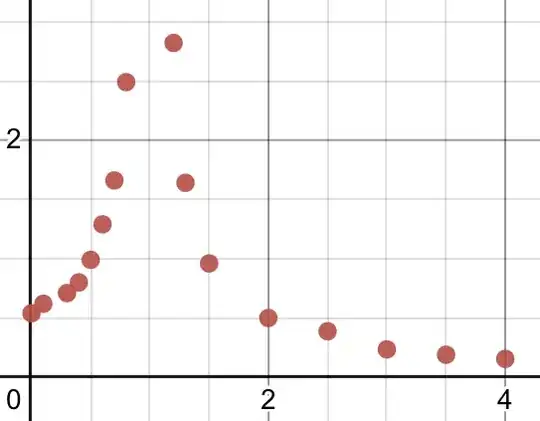
Here is a plot of the error between the $\delta(x)$ series approximation and Wolfram Alpha’s result: $$y\cot(y)=x,\lim_{N\to\infty}\frac1{2\pi}\int_0^\frac\pi2\sum_{n=-N}^N e^{i n(\tan(t)-xt)}dt-\frac1{\sec^2(y)-x}:$$

enter image description here

Finding the error term helps find the series solution to $y\cot(y)=x$. We know that the error when $x=2$ gives error$=\frac12$ and the error when $x=1$ diverges. However, there is no formula for $x>1$.

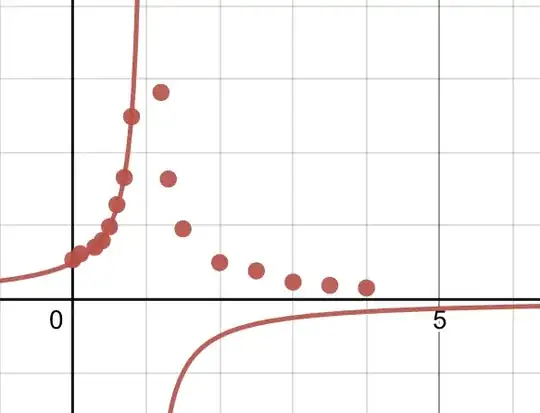
After tinkering, one finds the error for $0<x<1$ is $\frac1{2(\sec^2(0)-x)}=\frac1{2(1-x)}$:

enter image description here

Question

If possible, what is $\displaystyle\int_0^\frac\pi2\delta(\tan(t)-xt)dt,x>1$?

Тyma Gaidash
  • 12,081

2 Answers2

1

This may not be a complete answer, but illustrates a problem with using the Fourier series representation of $\delta(t)$ which is really the Fourier series of the Dirac comb.

Figure (1) illustrates the function

$f(t)=\tan (t)-2 t\tag{1}$

has a zero at $t=0$ as well as a zero at $t\approx 1.16556$.

f(t) defined in formula (1)

Figure (1): Illustration of $f(t)$ defined in formula (1)

Figure (2) illustrates $\delta(f(t))$ using the limit representation

$$\delta(t)=\underset{f\to\infty}{\text{lim}}\left(2 f\, \text{sinc}(2\, \pi f\, t)\right)\tag{2}$$

evaluated at $f=100$ has a $\delta$-function spike at $t=0$ as well as at $t\approx 1.16556$ corresponding to the two zeros of $f(t)$ mentioned above.

delta(f(t)) using formula (2)

Figure (2): Illustration of $\delta(f(t))$ using formula (2) for $\delta(t)$

Figure (3) illustrates $\delta(f(t))$ using the Fourier series representation

$$\delta(t)=\frac{1}{2 \pi}\underset{N\to\infty}{\text{lim}}\left(\sum\limits_{n=-N}^N \exp(i n t)\right),\quad -\pi<t<\pi\tag{3}$$

evaluated at $N=100$ exhibits interference from the teeth of the Dirac comb. This answer I posted to a related follow-up question illustrates this interference more clearly.

delta(f(t)) using formula (3)

Figure (3): Illustration of $\delta(f(t))$ using formula (3) for $\delta(t)$

I can't seem to derive a result for

$$\int\limits_0^{\frac{\pi}{2}} \delta(f(t))dt\tag{4}$$

using the limit representation for $\delta(t)$ defined in formula (2) above (except via numerical integration), but there are other limit representations that you could try (e.g. see here).

In general I don't believe an integral of $\delta(t)$ with a lower (or upper) integration bound of $t=0$ is well defined, but I believe many analytic representations of $\delta(t)$ will capture half of the contribution of the $\delta$-spike at $t=0$.

Mathematica indicates the following

$$\int_0^{\frac{\pi }{2}} \delta (\tan (t)-2 t) \, dt=\frac{1}{\sec ^2(\text{Root}[\{2 \text{$\#$1}-\tan (\text{$\#$1})\&,1.16556118520721130683\}])-2}\approx 0.225523\tag{5}$$

which ignores the contribution of the $\delta$-spike at $t=0$ illustrated in Figure (2) above.

Steven Clark
  • 7,363
  • After plotting, the “interference from the teeth” likely is the interference from the oscillation of $\cos(\tan(x))$ which oscillates faster as $x\to\frac\pi2$ – Тyma Gaidash Jan 29 '23 at 01:18
  • @TymaGaidash The argument $f(t)=\tan (t)-2 t$ of $\delta(f(t))$ in the integral $\int\limits_0^{\frac{\pi}{2}} \delta(f(t)),dt$ takes on all positive values in the interval $0<t<\frac{\pi}{2}$, so therefore the integral captures the contribution of all teeth of the Dirac comb in the right-half plane. The argument $f(t)$ also takes on a small range of negative values in the interval $0<t<\frac{\pi}{2}$, but this is less of a problem because it never goes far enough negative to reach the first tooth of the Dirac comb in the left-half plane which is at $-2 \pi$. – Steven Clark Jan 29 '23 at 03:38
0

After more work, we get the actual solution where $y$ is the smallest positive solution to $\tan(y)-xy=0$

$$\int_0^\frac\pi2\delta(\tan(t)-xt)dt=\frac1{\sec^2(y)-x}+\color{green}{\frac1{2|x-1|}}$$

Therefore:

$$\frac1{\sec^2(y)-x}=\int_0^\frac\pi2\delta(\tan(t)-xt)dt-\frac1{2|x-1|}$$

Graphically, the $\color{green}{\text{error}}$ term works for $x\ge0$ and maybe $x\in\Bbb R$:

enter image description here

Now to possibly solve $y\cot(y)=x$ by expanding the $\delta(w)$.

Тyma Gaidash
  • 12,081