$\int_{-\infty}^\infty \frac{e^{ax}}{1+e^x}dx$ /estimation vertical lines

Question

First of all, I know this very integral has been asked many times on this site (e.g $\int_{-\infty}^\infty \frac{e^{ax}}{1+e^x}dx$ with residue calculus) and I don't have any problem calculating the residue here and the value of integral.

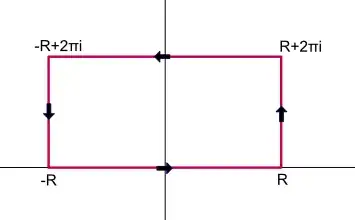
However I am struggeling in a part of this exercise, that is nowhere elaborated in good detail, namely to show that the two vertical lines $\to 0$ when $R \to \infty$ (see contour below) and in all the other threads it is only stated that it is clear that this happens, nowhere could I find a more detailed calculation.

Let $c_1(t)$ be the right vertical line (from $R \to R+2\pi i$) I have chosen the following parameterization: $c_1(t)=(1-t)R+(R+2\pi i)t = R +2\pi i t$, $t \in [0,1]$

$c_1'(t) = 2\pi i$ Let $c_3(t)$ be the left vertical line (from $-R+2\pi i \to -R$)

I have chosen the following parameterization:

$c_3(t)=(-R+2 \pi i)(1-t) + (-R)t=-R+2 \pi i(1-t)$, $t \in [0,1]$

$c_3'(t) = -2\pi i$

so for the right vertical line:

|$\int_0^1 \dfrac{e^{a(R+2\pi it)}}{1+e^{R+2\pi it}} 2\pi i dt | \leq 2\pi e^{aR} \int_{0}^{1} |\dfrac{e^{{(2 \pi i)}^{at}}}{1+e^Re^{(2\pi i)^t}}dt| \leq 2\pi e^{aR} \int_{0}^{1} \dfrac{1}{1+e^R} dt = 2\pi \dfrac{e^{aR}}{1+e^{R}}$ (are the steps here justified/correct?)

so for $R \to \infty$ clearly $2\pi \dfrac{e^{aR}}{1+e^{R}} \to 0$ because a < 1 (with l'Hôpital)

for the left vertical line: $|\int_{0}^{1} \dfrac{e^{a(-R)}e^{(2 \pi i)^{a}}e^{(2 \pi i)^{-t}}}{1+e^{-R}e^{2\pi i}e^{({2\pi i})^{-t}}} (-2\pi i) dt | \leq 2\pi\int_{0}^{1} |\dfrac{e^{a(-R)}e^{(2 \pi i)^{a}}e^{(2 \pi i)^{-t}}}{1+e^{-R}e^{2\pi i}e^{({2\pi i})^{-t}}}dt|=2 \pi \int_{0}^{1} \dfrac{e^{a(-R)}}{1+e^{-R}}dt$

are the steps until the last equality sign correct?

so I would need to calculate $\lim_{R \to \infty} \dfrac{e^{a(-R)}}{1+e^{-R}}$, but how to evaluate this and show that this will also be zero? I can not use l'Hôpital anymore. what would be the best way here?

Answer 1

Note that the integral in question is improperly integrable for $a \in (0,1)$. Using the parameterizations you mentioned above,

$$ \eqalign{ 0 &\leq \left|\int_{R}^{R+2\pi i}f\left(z\right)dz\right| \cr &= \left|\int_{0}^{1}f\left(R+2\pi it\right)d\left(R+2\pi it\right)\right| \cr &\leq 2\pi\int_{0}^{1}\left|f\left(R+2\pi it\right)\right|dt \cr &= 2\pi\int_{0}^{1}\left|\frac{e^{aR}e^{2\pi it}}{1+e^{R}e^{2\pi it}}\right|dt \cr &\leq 2\pi e^{aR}\int_{0}^{1}\frac{1}{e^R-1}dt \text{ (Can you see your mistake?)} \cr &= \frac{2\pi e^{aR}}{e^{R}-1}. \cr } $$ As $R \to \infty$, that last expression goes to $0$. Then you use the Squeeze Theorem to prove that $\displaystyle \int_{R}^{R+2\pi i}f\left(z\right)dz \to 0$ as $R \to \infty$.

Similarly,

$$ \eqalign{ 0 &\leq \left|\int_{-R}^{-R+2\pi i}f\left(z\right)dz\right| \cr &= \left|\int_{1}^{0}f\left(-R+2\pi i\left(1-t\right)\right)d\left(-R+2\pi i\left(1-t\right)\right)\right| \cr &= 2\pi\left|\int_{0}^{1}\frac{e^{-aR}e^{2\pi i\left(1-t\right)}}{1+e^{-R}e^{2\pi i\left(1-t\right)}}dt\right| \cr &\leq 2\pi e^{-aR}\int_{0}^{1}\left|\frac{e^{2\pi i\left(1-t\right)}}{1+e^{-R}e^{2\pi i\left(1-t\right)}}\right|dt \cr &\leq 2\pi e^{-aR}\int_{0}^{1}\frac{1}{1-e^{-R}}dt \cr &= \frac{2\pi e^{-aR}}{1-e^{-R}}. \cr } $$ (Can you see your mistakes?) Then $$\lim_{R \to \infty}\frac{2\pi e^{-aR}}{1-e^{-R}} = \frac{0}{1-0} = 0.$$ Use the Squeeze Theorem to prove $\displaystyle \int_{-R}^{-R+2\pi i}f\left(z\right)dz \to 0$ as $R \to \infty$ and you're done.

Please let me know if there are questions.

Answer 2

Accelerator's answer is very nice, and already corrects your mistakes, so instead of focusing on that, I'll offer an alternative way.

First, note that we must set the restriction of $0<\Re(a)<1$ for your integral to converge.

Next, not dissimilar to my answer here, we will parameterize the contours and use the triangle ineq for integrals along with various other variants of the triangle inequalities detailed below. $$|a+b|\le|a|+|b|\Longleftrightarrow|a-b|\ge||a|-|b||\Longleftrightarrow\frac1{|a-b|}\le\frac1{||a|-|b||}$$

Call the left path $L$, and right path $\mathcal R$. Then, parameterizing them gives \begin{alignat*}{5} \mathcal{R}&:\text{ }z=R+iy,\qquad &\text{d}z&=i\text{ d}y,\qquad &y&\in[0, 2\pi]\\ L&:\text{ }z=-R+iy,\qquad &\text{d}z&=i\text{ d}y,\qquad &y&\in[2\pi, 0] \end{alignat*}

where $R$ is some arbitrarily large real number that goes to infinity.

Starting with $\mathcal R$, we have (all in red goes to 1 and thus cancels) \begin{align} \left|\int_{\mathcal{R}}f(z)\text{ d}z\right|&\le\int^{2\pi}_0\frac{\left|e^{aR}\right|{\color{red}{\left|e^{aiy}\right|}}}{\left|e^Re^{iy}+1\right|}\cdot{\color{red}{|i|}}\text{ d}y\\ &\le\int^{2\pi}_0\frac{e^{|a|R}}{\left|\left|e^R\right|{\color{red}{\left|e^{iy}\right|}}-|-1|\right|}\text{ d}y\\ &=\int^{2\pi}_0\frac{e^{|a|R}}{e^R-1}\text{ d}y=\frac{2\pi e^{|a|R}}{e^R-1} \end{align}

Taking the limit gives $$\lim_{R\to+\infty}\frac{2\pi e^{|a|R}}{e^R-1}=0$$ with our restricted $a$ and thus proves that the integral about $\mathcal{R}$ vanishes.

Using the same arguments for $L$, we have \begin{align} \left|\int_Lf(z)\text{ d}z\right|&\le\int^{0}_{2\pi}\frac{\left|e^{-aR}\right|{\color{red}{\left|e^{aiy}\right|}}}{\left|e^{-R}e^{iy}+1\right|}\cdot{\color{red}{|i|}}\text{ d}y\\ &\le\int^{0}_{2\pi}\frac{e^{-|a|R}}{\left|\left|e^{-R}\right|{\color{red}{\left|e^{iy}\right|}}-|-1|\right|}\text{ d}y\\ &=\int^{2\pi}_0\frac{-e^{-|a|R}}{\left|e^{-R}-1\right|}\text{ d}y=\frac{-2\pi e^{-|a|R}}{1-e^{-R}} \end{align}

Taking the limit will yield $$\lim_{R\to+\infty}\frac{-2\pi e^{-|a|R}}{1-e^{-R}}=0$$

Hence both integrals along the sides will go to zero since their absolute upper bound is also zero.

Hopefully this makes sense! :)