There are some calculations you make that I can't follow, but the idea makes sense to me. Maybe you should check the limits of integration, supports, etc. I will write a version of the solution as I commented previously with an idea that I once learned from a friend. The idea is basic: work on $[0,1]$ taking advantage of uniformity and use definitions moving to $[0,L]$.
Suppose $X,Y\sim U[0,L]$ for $L>0$. Then notice that transformation $$(Z_1,Z_2)\to\left(\frac{1}{L}X,\frac{1}{L}Y\right) \implies Z_1,Z_2\sim U(0,1).$$
Thus for $t\in [0,L]$, we have
$$P(|X-Y|\leqslant t)=P(|LZ_1 -LZ_2 |\leqslant t)=P(|Z_1-Z_2)|\leqslant t/L),\quad (*)$$
Thus, it is sufficient to work with $X, Y\sim U[0,1]$ and then use $(*)$ to conclude with the result. Indeed, suppose that $X,Y\sim U(0,1)$ and by independence the joint density is given by
$$f(x,y)=\begin{cases}1,\quad 0\leqslant x,y\leqslant 1,\\0\quad \text{otherwise}\end{cases}$$
We want $P(|X-Y|\leqslant t)$ for $t\in [0,1]$. But, by complement we have $$P(|X-Y|\leqslant t)=1-P(|X-Y|\geqslant t)$$
Thus, it is sufficient to find $\boxed{P(|X-Y|\geqslant t)}$.
Since we want to find $P(|X-Y|\geqslant t)$ for $t\in [0,1]$ so we need to know the points $(x,y)$ so that $|x-y|\geqslant t$. The easy way is to locate the points that divide the regions $x-y\geqslant t$ or $x-y\leqslant -t$. These points are on the straight lines $|x-y|=t$ that is $x-y=t$ or $-(x-y)=t$, a first plot it useful.
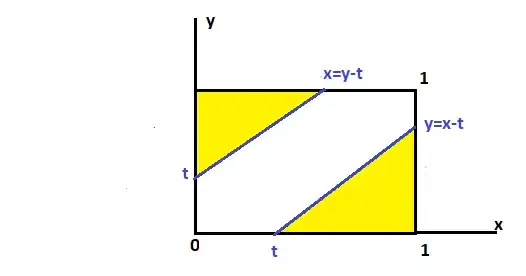
It is easier to use geometry here, but we can continue using of the definition, so we need to use doubles integrals.
$$P(Y-X\geqslant t)=\int_{t}^{1}\int_{0}^{y-t}1\, dxdy=\frac{(t-1)^{2}}{2}$$
$$P(X-Y\geqslant t)=\int_{t}^{1}\int_{0}^{x-t}1\, dydx=\frac{(t-1)^{2}}{2}$$
Thus, $$P(|X-Y|\leqslant t)=1-P(|X-Y|\geqslant t)=\boxed{1-P(Y-X\geqslant t)-P(X-Y\geqslant t)}$$
give $$\boxed{P(|X-Y\leqslant t)=1-(t-1)^{2}}$$
The probability density function is given so $$\boxed{f(t)=\begin{cases}2-2t, 0\leqslant t\leqslant 1,\\0,\quad \text{otherwise}\end{cases}}$$
Using $(*)$, then we have $P(|X-Y|\leqslant t/L)=1-(t/L-1)^{2}$ and taking the derivative we find the probability density function $$\boxed{f(t)=\begin{cases} 2(L-t)/L^{2}\quad 0\leqslant t\leqslant L,\\0,\quad \text{otherwise}\end{cases}}$$
