Find the intersection points of two circles

Question

Find the intersection points of the circles $$k_1:(x-4)^2+(y-1)^2=9\\k_2:(x-8)^2+(y+4)^2=100$$

The intersections point (if they exist) will satisfy the equations of both the circles, so we can find their coordinates by solving the system $$\begin{cases}(x-4)^2+(y-1)^2=9\\(x-8)^2+(y+4)^2=100\end{cases}\iff\begin{cases}x^2-8x+y^2-2y=-8\\x^2-16x+y^2+8y=20\end{cases}$$ Substracting these equations, gives $4x-5y=-14\Rightarrow x=\dfrac{5y-14}{4}$. Substituting into the first, I got (if I didn't mess up the calculations) $$41y^2-332y+766=0$$ which has no real solutions (negative discriminant). Therefore the system has no solutions as well, so the circles don't intersect. Is there something else we can use in order to conclude that they do not intersect? Maybe something which requires less calculations? The center of the first is $O_1(4;1)$, the center of the second cirlce is $O_2(8;-4)$ and their radii are $r_1=3$ and $r_2=10$, respectively, if this somehow helps. The distance $O_1O_2=\sqrt{16+25}=\sqrt{41}$ and $r_1+r_2=13=\sqrt{169}$, but I am not sure how to interpret these findings.

Answer 1

The distance between the centers is $d(O_1,O_2)=\sqrt{(8-4)^2+(1+4)^2}<7$ if they had an intersection point $p$ than $7>d(O_1,O_1)\geq|d(O_1,p)-d(O_2,p)|=|10-3|=7$
In general, two circles intersect iff $|r_1-r_2|\leq d\leq r_1+r_2$

Answer 2

Geometric point of view: The radical axis of two circles passes through the intersection points of the circles when they intersect. If we show that the distance of the centers of the circles to that line is larger than their radii, we're done.

You found the radical axis. It is $L:4x-5y+14=0$. Now, $h_1=d(L,O_1)=\frac{|4\times4-5\times1+14|}{\sqrt{4^2+5^2}}=\frac{25}{\sqrt{41}}>\frac{25}{7}>3=R_1$ and similarly $h_2=d(L,O_2)==\frac{|4\times8-5\times(-4)+14|}{\sqrt{4^2+5^2}}=\frac{66}{\sqrt{41}}>10=R_2$, since $66^2=4356>4100.$

Answer 3

Any point on the first circle : $P(4+3\cos t,1+3\sin t)$

If $P$ has to be on the second circle as well, $$100=(4+3\cos t-8)^2+(1+3\sin t+4)^2=-24\cos t+30\sin t+16+25$$

$$\iff5\sin t-4\cos t=\dfrac{41}6$$

Now $|5\sin t-4\cos t|\le\sqrt{4^2+5^2}=\sqrt{41}$ which is $<\dfrac{41}6$ as $6<\sqrt{41}$

So, no real intersection!

Answer 4

If you're familiar with implicit differentiation, we can locate the points where the slopes of the tangent lines to the two circles "match". We have $$ (x \ - \ 4)^2 \ + \ (y \ - \ 1)^2 \ \ = \ \ 9 \ \ \Rightarrow \ \ 2·(x \ - \ 4) \ + \ 2·(y \ - \ 1)·y' \ \ = \ \ 0 \ \ \Rightarrow \ \ y' \ \ = \ \ \frac{4 \ - \ x}{y \ - \ 1 } \ \ , $$ $$ (x \ - \ 8)^2 \ + \ (y \ + \ 4)^2 \ \ = \ \ 100 \ \ \Rightarrow \ \ 2·(x \ - \ 8) \ + \ 2·(y \ + \ 4)·y' \ \ = \ \ 0 \ \ \Rightarrow \ \ y' \ \ = \ \ \frac{8 \ - \ x}{y \ + \ 4 } \ \ . $$

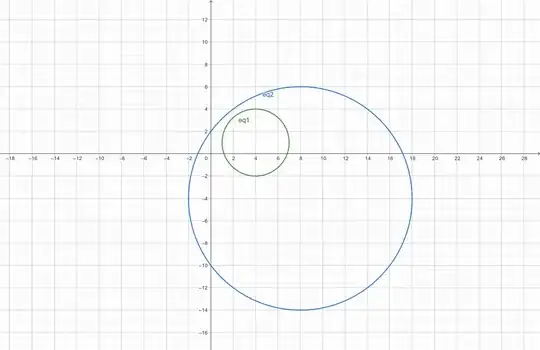
The slopes agree for $$ \frac{4 \ - \ x}{y \ - \ 1 } \ \ = \ \ \frac{8 \ - \ x}{y \ + \ 4 } \ \ \Rightarrow \ \ 24 \ - \ 5x \ \ = \ \ 4y \ \ . $$ This turns out to be the line [in green in the graph below] passing through the centers of the two circles ($ \ 5·4 + 4·1 \ = \ 5·8 + 4·(-4) $ $ = \ 24 \ $ ). Upon inserting $ \ y \ = \ 6 - \frac54·x \ $ into the equations of the circles, we obtain $$ ( \ x \ - \ 4 \ )^2 \ + \ \left( \ \left[6 - \frac54·x \right] \ - \ 1 \right)^2 \ \ = \ \ 9 \ \ \Rightarrow \ \ \frac{41}{16}·x^2 \ - \ \frac{41}{2}·x \ + \ 32 \ = \ 0 $$ $$ \ \ \Rightarrow \ \ x \ \ = \ \ 4 \ \pm \ \frac{12}{\sqrt{41}} \ \ \ , \ \ \ y \ \ = \ \ 1 \ \mp \ \frac{15}{\sqrt{41}} \ \ \rightarrow \ \ ( \ \approx 2.13 \ , \ \approx 3.34 \ ) \ \ , \ \ ( \ \approx 5.87 \ , \ \approx -1.34 \ ) \ \ ; $$ $$ ( \ x \ - \ 8 \ )^2 \ + \ \left( \ \left[6 - \frac54·x \right] \ + \ 4 \right)^2 \ \ = \ \ 100 \ \ \Rightarrow \ \ \frac{41}{16}·x^2 \ - \ 41·x \ + \ 64 \ = \ 0 $$ $$ \ \ \Rightarrow \ \ x \ \ = \ \ 8 \ \pm \ \frac{40}{\sqrt{41}} \ \ \ , \ \ \ y \ \ = \ \ -4 \ \mp \ \frac{50}{\sqrt{41}} \ \ \rightarrow \ \ ( \ \approx 1.75 \ , \ \approx 3.80 \ ) \ \ , \ \ ( \ \approx 14.25 \ , \ \approx -11.81 \ ) \ \ . $$

From this, we see that along the line $ \ y \ = \ 6 - \frac54·x \ \ , \ $ which has negative slope, both of the "tangent points" for the smaller circle are "to the right and below" (larger $ \ x-$ and smaller $ \ y-$coordinates) of the leftmost "tangent point" of the larger circle and "to the left and above" its rightmost "tangent point". The smaller circle must then be entirely within the interior of the larger circle, so they have no intersections.

If one pair of these coordinates for each circle were the same, it would identify a point of mutual tangency, which would be the single intersection between them. With this "slope-matching" line having negative slope,

• if one pair of coordinates for the smaller circle were "to the left and above" one pair for the larger circle and the other pair were "to the right and below" the same pair for the larger circle, this would tell us that the smaller circle "straddles" the boundary of the larger circle and we would find two intersection points for the circle;

• if both pairs of coordinates for the smaller circle are "to the right and above" or "to the left or below" those of the larger circle, the smaller circle is entirely exterior to the larger circle, and again we should expect there to be no intersections.

We would make corresponding adjustments to this description if the "slope-matching" line had positive slope.

$$ \ \ $$

The "intersection line" $ \ 4x - 5y \ = \ -14 \ $ [in orange in the graph] that you found passes just "outside" of the larger circle, so there are no real intersection points for the circles. (If we translated the smaller circle until it made a point of mutual tangency with the larger one, we would see the intersection line also translate until it became tangent at that point.) Inserting either $ \ y \ = \ \frac{4x \ + \ 14}{5} \ $ or $ \ x \ = \ \frac{5y \ - \ 14}{4} \ $ into either circle equation produces for both of them $$ 41·x^2 \ - \ 128·x \ + \ 256 \ \ = \ \ 0 \ \ \Rightarrow \ \ x \ \ = \ \ \frac{64}{41} \ \pm \ \frac{80}{41}·i \ \ \ , $$ $$ 41·y^2 \ - \ 332·y \ + \ 772 \ \ = \ \ 0 \ \ \Rightarrow \ \ y \ \ = \ \ \frac{166}{41} \ \pm \ \frac{64}{41}·i \ \ \ , $$ these coordinate values being consistent with $ \ 4x - 5y \ = \ -14 \ \ . \ $ [I am not getting your constant term in the $ \ y-$coordinate quadratic polynomial, but what you have does not affect your conclusion.] These intersection points can be better understood if we consider the "circle" equations in $ \ \mathbb{C}^2 \ \ , \ $ (where the equations describe two surfaces in four (real) dimensions), rather than just in $ \ \mathbb{R}^2 \ \ $ (but we won't go into that here).